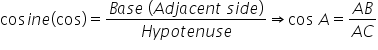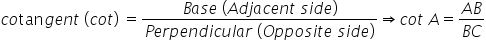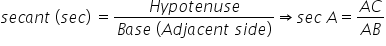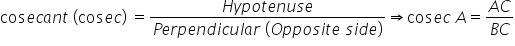Importance of trigonometry and its applications

Fields of study which use trigonometry or trigonometric functions are many, and the ICSE Class 10 Maths curriculum includes the chapter of Trigonometry because it finds applications which would make any serious student of Math or Engineering to sit up.

By Topperlearning Expert 14th Aug, 2020 | 04:55 pm

Basics of trigonometry

Trigonometry is a branch of Mathematics which focuses on the relationships between the sides and angles of triangles. It involves various trigonometric functions, and those functions are used for the determination of unknown angles and sides of a triangle.

Trigonometry has been included in the ICSE Class 10 curriculum because it is one of the chapters of Mathematics which has the most applications. Knowledge of trigonometric functions and identities is also necessary to understand subjects taught in higher level Math courses.

Common applications of trigonometry

We are actually surrounded by various applications of trigonometry, but we are unaware of them. For example, trigonometry is used in the construction of houses and cars. Well, not in the entire process of construction, but certain concepts and measurements based on trigonometry are used. In fact, technology used in medical imaging, computer graphics etc. is developed and manufactured using trigonometry.

Trigonometry plays a very important role in dealing with triangles, especially right-angled triangles.

Let’s discuss some geometrical applications of trigonometry.

The geometrical applications of trigonometry generally focus on the calculation of sides and angles of a right-angled triangle. The exact measurement of an angle is obtained using trigonometry.

There are six trigonometric ratios which depict the relationships between the sides and angles of a right-angled triangle. The ratios for a right-angled triangle ABC are as follows:

$sin e left parenthesis sin right parenthesis equals fraction numerator P e r p e n d i c u l a r space left parenthesis O p p o s i t e space s i d e right parenthesis over denominator H y p o t e n u s e end fraction rightwards double arrow sin space A equals fraction numerator B C over denominator A C end fraction$
$cos i n e left parenthesis cos right parenthesis equals fraction numerator B a s e space left parenthesis A d j a c e n t space s i d e right parenthesis over denominator H y p o t e n u s e end fraction rightwards double arrow cos space A equals fraction numerator A B over denominator A C end fraction$
$tan g e n t left parenthesis tan right parenthesis equals fraction numerator P e r p e n d i c u l a r space left parenthesis O p p o s i t e space s i d e right parenthesis over denominator B a s e space left parenthesis A d j a c e n t space s i d e right parenthesis end fraction rightwards double arrow tan space A equals fraction numerator B C over denominator A B end fraction$
$c o tan g e n t space left parenthesis c o t right parenthesis space equals fraction numerator B a s e space left parenthesis A d j a c e n t space s i d e right parenthesis over denominator P e r p e n d i c u l a r space left parenthesis O p p o s i t e space s i d e right parenthesis end fraction rightwards double arrow c o t space A equals fraction numerator A B over denominator B C end fraction$
$s e c a n t space left parenthesis s e c right parenthesis space equals fraction numerator H y p o t e n u s e over denominator B a s e space left parenthesis A d j a c e n t space s i d e right parenthesis end fraction rightwards double arrow s e c space A equals fraction numerator A C over denominator A B end fraction$
$cos e c a n t space left parenthesis cos e c right parenthesis space equals fraction numerator H y p o t e n u s e over denominator P e r p e n d i c u l a r space left parenthesis O p p o s i t e space s i d e right parenthesis end fraction rightwards double arrow cos e c space A equals fraction numerator A C over denominator B C end fraction$

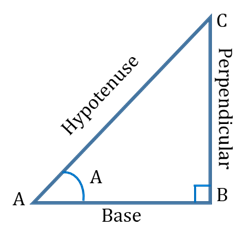
Few important points to note about trigonometry:

Each trigonometric ratio is a real number with no unit.
Values of trigonometric ratios are always the same for the same angles.

Let’s now focus on certain analytical uses of trigonometry:

The most effective and progressive use of trigonometry is to analyse and simplify equations using various trigonometric functions like sine, cosine, tangent etc. Analytical use of trigonometry plays a vital role in engineering fields like mechanical engineering, electronics and mechatronics. Before moving ahead to some more applications of trigonometry, let’s look at trigonometric identities and the related terms.

Trigonometric identities

These are basically the equations involving trigonometric ratios of an angle, which is true for all the values of that particular angle. These are sometimes confusing to understand; however, they can be used to determine all the trigonometric values and derivations. Basically, both sides of the equation are equal and can be swapped to determine the trigonometric values.

Some of the basic trigonometric identities are

a) sin²A + cos²A = 1 b) 1 + tan²A = sec²A c) 1 + cot²A = cosec²A

Real-life applications of trigonometry

Developed primarily for the purpose of navigation, trigonometry is mainly used by satellite systems and in the field of astronomy. It is also used in aviation and naval industries, land surveys, oceanography and cartography. The objective of using trigonometry is to measure distances accurately.

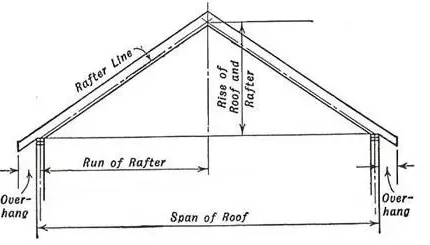
There are many direct applications of trigonometry in activities of daily life. One such application is a mechanical structure like a building or a bridge. The blueprint of its plan involves a lot of trigonometric concepts where the necessary measurements are done. Trigonometry makes it possible to determine unknown angles and sides. This is very important for drafting a plan as shown in the sketch below. Trigonometry finds a perfect partner in modern architecture.

The angle of elevation is a trigonometric property used in many sectors. Height, distance and surface area, all these need the application of this property.

Trigonometry is also used in music production. While conducting sound waves, the trigonometric identities sine and cosine come into play, where the basic laws of sine and cosine have to be applied. Trigonometry is also a silent guest when conductors or producers measure sound waves. Sometimes, panels are used to make sound waves bounce off walls.

Trigonometry plays an important role in computer imaging. It is broadly used to generate detailed and complex images using a computer. The process of generating such detailed images is known as triangulation. In this process, several trigonometric concepts are used.

One of the most famous and important applications of trigonometry is measuring the height of mountains. The height of the very popular Mount Everest has also been measured using the trigonometric concept ‘trigonometry and shadows’.

Some of the other fields which use trigonometry or trigonometric functions are

Electronics, Biology, Medical Imaging (CT scan, ultrasound), Chemistry, Number Theory, Cryptology, Metrology, Oceanology, Image Compression, Phonetics, Economics, Engineering (Electrical, Mechanical, Civil), Computer Graphics, Cartography, Crystallography and Game Development.

Trigonometry is a very important part of ICSE Class 10 Mathematics and integrates memorisation, conceptual understanding and problem-solving ability. It helps students to have a better understanding of the world because many of the earth’s natural structures resemble triangles. Although trigonometry is most applicable for right-angled triangles, it can also be used for other types of triangles.

Trigonometry should be understood clearly at its introductory stage to develop a strong base which will prove beneficial in the long run.

Start your new academic year with TopperLearning’s study resources. Get seamless access to sample papers, past years’ papers, most important questions, video lessons, mock tests, weekly tests and much more. Call our academic consultant on 9372462318 or visit TopperLearning.

CBSE Class 10 study resources

CBSE Class 12 Science study resources

CBSE Class 12 Commerce study resources

ICSE Class 10 study resources

JEE Main 2021 study resources

NEET 2021 study resources