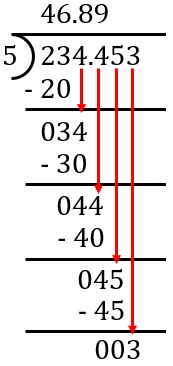
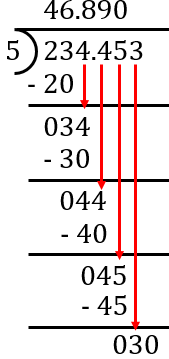
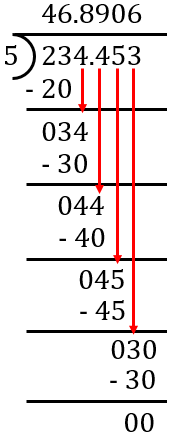
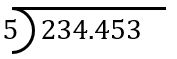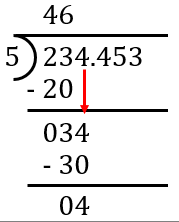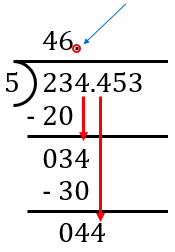ICSE Class 10 Division of Decimal Numbers - Common Mistakes to Avoid
Important Resources
- Education Franchisee opportunity
- NCERT Solution
- CBSE Class 9 Mathematics
- NCERT Solutions for class 10 Science
- Sample Papers
- CBSE Class 9 Science
- NCERT Solutions for class 10 Maths
- Revision Notes
- CBSE Class 10 Hindi
- CBSE Class 10 English
- CBSE Class 10 English
- CBSE Class 10 Social Studies
- CBSE Class 10 Science
- CBSE Class 10 Mathematics
- Career In Science After 10
- Career In Commerce After 10
- Career In Humanities/Arts After 10
- NCERT Solutions for Class 10
- NCERT Solutions for Class 11
- Business Studies Class 12 CBSE project