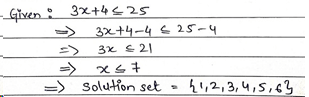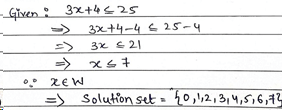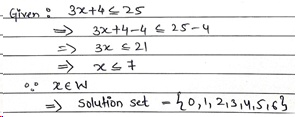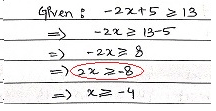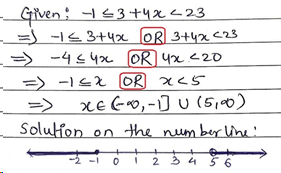Common Mistakes Made In ICSE Class 10 Board Exams - Chapter Linear Inequalities

Common Mistakes Made in ICSE Class 10 Board Exams - Chapter Linear Inequalities

In this blog, we'll explore the errors made by the students in Linear Inequation questions to help you avoid them. Before discussing the errors, we'll learn about the basics of Linear Inequalities and the methods to solve them.

By Topperlearning Expert 22nd Jan, 2024 | 03:45 pm

Linear inequalities are the helpful tools for interpreting variable relationships in the area of Mathematics. However, as the students set out to solve these inequalities, frequent mistakes can convert a simple task into a confusing maze. Minimize these mistakes by joining us on an exploration of the common pitfalls that often elude pupils. Let's set out to achieve mathematical clarity and arm ourselves with the understanding necessary to overcome problems on linear inequality.

Overview of Linear Inequations:

Various Linear Inequations

1^st : x > y

Eg: 4 < 5

2^nd : x ≥ y

Eg: y ≥ 6

3^rd : x < y

Eg: x – 4 < y + 9

4^th : x ≤ y

Eg: x + 5 ≤ 10

Important Terms:

> : read as, greater than

≥ : read as, greater than or equal to

< : read as, less than

≤ : read as, less than or equal to

Solving Linear Inequations

Rule 1	• On transferring a positive term from one side of an inequation to its other side, the sign of the term becomes negative. • Example: 4x + 5 > 6 ⇒ 4x > 6 – 5
Rule 2	• On transferring a negative term from one side of an inequation to its other side, the sign of the term becomes positive. • Example: 4x – 5 > 6 ⇒ 4x > 6 + 5
Rule 3	• If each term of an inequation be multiplied or divided by the same positive number, the sign of inequality remains the same. • Example: x < 5 ⇒ 3x < 15
Rule 4	• If each term of an inequation be multiplied or divided by the same negative number, the sign of inequality reverses. • Example: x < 5 ⇒ –3x > –15
Rule 5	• If sign of each term on both the sides of an inequation is changed, the sign of inequality gets reversed. • Example: x < –5 ⇒ –x > 5
Rule 6	• If both the sides of an inequation are either positive or negative, then on taking their reciprocals, the sign of inequality reverses. • Example: x < y ⇒

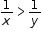
Replacement Set and Solution Set

Replacement set is the set from which the values of the variable involved in the inequation are chosen.

Solution set is the subset of the replacement set, whose elements satisfy the given inequation.

For inequation, x ≤ 4.

Replacement set = N, the set of natural numbers

For inequation, x ≤ 4.

Solution set = {1, 2, 3, 4}

Representation on the number line

i. The solution set of an inequation can be represented on a real number line.

ii. A hollow circle marks the end of a range with a strict inequality (< or >).

iii. A darkened circle marks the end of a range involving an equality as well (≤ or ≥).

Example:
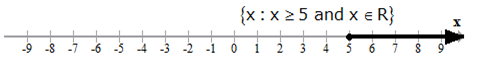
Remember

1. If the product of two numbers is negative, then one of the two numbers is positive and other one is negative.

2. If the product of two numbers is positive, then both the numbers are either positive or negative.

Let’s now start discussing the mistakes made by students.

Mistake 1: Students don’t include end values for ≤ or ≥

When the inequality ≥ or ≤ is given, we must include the end values.

The question is to find the solution set of the inequation 3x + 4 ≤ 25, where x ∊ W.

Solution(s) with mistake

Solution 1

Correct Solution

Solution 2

The end value ‘7’ and whole number ‘0’ are not included in the set.

Solution 3

The end value ‘7’ is not included in the set.

End value ‘7’ is included. Also, ‘0’ is included as x belongs to the set of whole numbers.

Mistake 2: Does not change the inequality when changing signs

When we change the signs of the terms on both the sides of the inequality, it is necessary to change the sign of inequality as well.

This is shown with an example where we have given the inequation –2x + 5 ≥ 13, where x ∊ R.

Solution with mistake

Correct Solution

Solution 4

Sign changed from ‘-ve’ to ‘+ve” and vice versa, but didn’t change the sign of the inequality, resulting into incorrect values for ‘x’.

Solution 5

Mistake 3: Not changing signs while transposing like terms on the other side

Many students group the like terms on one side by transposing them but forget to change the sign of the terms as shown below with an example:

Solution with mistake

Solution 6

Correct Solution

Number ‘3’ was transferred to LHS in the 1^st case and to RHS in the 2^nd case but sign remains the same.

Mistake 4: Considering ‘OR’ instead of ‘AND’ when splitting the inequality

Many a times we separate the two conditions of an inequality with the constraint ‘OR’ instead of ‘AND’. By this, we take union of the values of x instead of taking intersection of those values.

This is shown below with an example where we need to represent the solution set of the inequality ‘–1 ≤ 3 + 4x < 23’ on the number line.

Solution with mistake

Solution 8

Correct Solution

Solution 9

OR is considered which results into incorrect solution set.

Mistake 5: Does not show the arrows on the number line

This is a very silly and common mistake students do while representing the solution on the number line.

Solution with mistake

Solution 10

Correct Solution

Solution 11

Arrow on each side of the number line represents that the line goes on and so it is necessary to show them.

Conclusion:

These were the few common mistakes observed among students while solving questions based on Linear inequalities. To avoid losing marks in the examination, steer clear of these errors. It is advisable to look for the inequality sign before proceeding or concluding the result, be careful of the signs while transposing or changing the inequality. Also, have clarity on using ‘AND’ and ‘OR’ statements when splitting the inequality. Therefore, strive to minimize errors by practising more questions. Stay tuned with TopperLearning for upcoming blogs on similar topics.

1^st : x > y

Eg: 4 < 5

2^nd : x ≥ y

Eg: y ≥ 6

3^rd : x < y

Eg: x – 4 < y + 9

4^th : x ≤ y

Eg: x + 5 ≤ 10