CBSE Class 11-science Answered
What is the centre of mass of arc of semicircle and arc of circle?explain briefly with diagram
Asked by rushabhjain.a | 24 Oct, 2019, 01:52: PM

Figure-1 shows a semi circle of radius R. Let the centre of curvature of arc coincide with the origin of the coordinate system.
Let us consider a small element of length dl at angular position θ and this elment of length dl subtends angle dθ.
Lenth of the small element = dl = R dθ .
Let ρ be the linear density , i.e. mass per unit length. Mass of the small element = R dθ × ρ
By symmetry, centre of mass (CM) is along y-axis, i.e, x-coordinate CX of CM is zero.
Y-coordinate CY of Centre of mass of semi-circular arc is obtained as
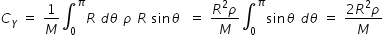 ................(1)
................(1)where M is total mass of semi-circular arc . we have, M = ρ×π R
By substituting for mass M in eqn.(1), we get, CY = 2R/π .......................(2)
Hence Centre of mass of semi-circle as shown in fig.(1) :- [ CX , CY ] = [ 0, (2R)/π ]
Centre of mass is at symmetry axis at a distance (2R)/π from centre of curvature of semi-circle.
-------------------------------------------------------------------------------------------------------------------------------------
Figure-2 shows a circular arc that subtends angle φ at centre .
Let the axis of symmetry coincide with x-axis of coordinate system and centre of curvature of circular arc coincide with origin.
Let us consider small element of arc of legth dl at angular position θ.
Let this small element subtends angle dθ at centre as shown in figure.
By symmetry, centre of mass is at x-axis, i.e., y-coordinate CY of centre of mass is zero.
x-coordinate Cx is obtained as follows
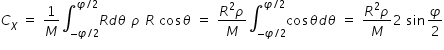 .......................(1)
.......................(1)In the above eqn. mass of arc , M = R φ ρ . By substituting mass in eqn. (1), we get, CX = ( 2R/φ ) sin(φ/2)
Hence centre of mass of arc as shown in figure-2 is, [ CX , CY ] = [ ( 2R/φ ) sin(φ/2) , 0 ]
Answered by Thiyagarajan K | 24 Oct, 2019, 09:42: PM
CBSE 11-science - Physics
Asked by sheikhsaadat24 | 17 Apr, 2024, 09:41: PM
CBSE 11-science - Physics
Asked by sy123946 | 07 Apr, 2024, 04:23: PM
CBSE 11-science - Physics
Asked by derhebha955 | 03 Apr, 2024, 09:03: AM
CBSE 11-science - Physics
Asked by sumedhasingh238 | 29 Mar, 2024, 05:15: PM
CBSE 11-science - Physics
Asked by sumedhasingh238 | 28 Mar, 2024, 11:10: PM
CBSE 11-science - Physics
Asked by roshnibudhrani88 | 23 Mar, 2024, 05:52: PM
CBSE 11-science - Physics
Asked by emad.amd | 21 Mar, 2024, 12:00: PM
CBSE 11-science - Physics
Asked by vinitdubey7735 | 14 Mar, 2024, 11:21: AM
CBSE 11-science - Physics
Asked by om636694 | 04 Mar, 2024, 09:10: PM
CBSE 11-science - Physics
Asked by rajuinwati12 | 04 Mar, 2024, 09:22: AM




