CBSE Class 12-science Answered

Let the factory at P transports x units of commodity to depot at A and y units to depot at B. Then, the mathematical model to the LPP is as follows :

Now, the weekly requirement of the depot at A is 5 units of the commodity. Since x units are transported from the factory at P, the remaining (5 – x) units need to be transported from the factory at Q. Obviously, 5 – x ≥ 0, i.e. x ≤ 5.

Similarly,

(5 – y) and 6 – (5 – x + 5 – y) = x + y – 4 units are to be transported from
the factory at Q to the depots at B and C respectively.

Thus, 5 – y ≥ 0 , x + y – 4 ≥0
i.e.      y ≤ 5 , x + y ≥ 4

Total transportation cost Z is given by :

Z = 16x + 10y +1 0(5-x) + 12(5-y) + 10(x+y-4) + 15(8-x-y)

   = x - 7y + 190

          Minimize Z = x - 7y + 190

Subject to     x + y < 8

                   x + y < 4

                         x < 5

                         y < 5

and              x > 0, y > 0

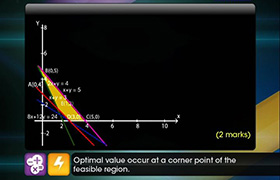
To solve this LPP graphically, we first convert the in equations into equations and draw the corresponding lines. The feasible region of the LPP is shaded in Fig

The coordinates of the corner points of the feasible region A₂ A₃ PQ B₃ B₂ are A₂ (4, 0), A₃ (5, 0), P(5, 3), Q (3, 5), B₃ (0, 5) and B₂ (0, 4). These points have been obtained by solving the corresponding intersecting line simultaneously.

The values of the objective function at these points are given in the following table :

Clearly, Z is minimum at x = 0, y = 5. The minimum value of Z is 155.

Thus, the optimal transportation strategy will be to deliver 0, 5 and 3 units from the factory at P and 5, 0  and 1 unit from the factory at Q to the depots at A, B and C respectively. The minimum transportation cost in this case in Rs 155.