CBSE Class 12-science Answered
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 300 is made on each economy class ticket. The airline reserves at least 20 seats for first class. However, at least 4 times as many passengers prefer to travel by economy class to by the first class. Determine how many each type of ticket must be sold in order to maximum the profit for the airline. What is maximum profit?
Asked by Topperlearning User | 31 Jul, 2016, 19:21: PM
Let x and y be the numbers of first class tickets and economy class tickets respectively we have the following LPP
Maximum 400x + 300y
st x + y ![]() 200
200
x ![]() 20
20
y ![]() 4x
4x
x ![]() 0, y
0, y ![]() 0
0
Let us draw the graph of the above LPP
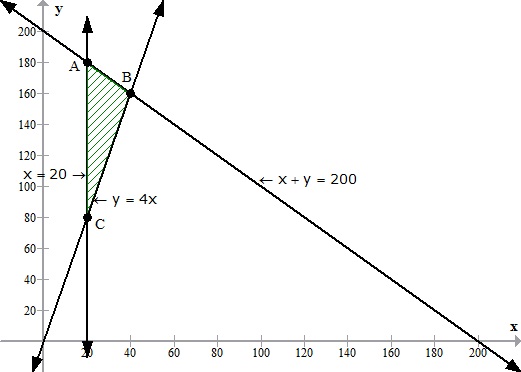
Thus, the feasible region is ABC and the corner points are A(20,180), B(40,160) and C(20,80)
The value of the objective function at the corner points are:
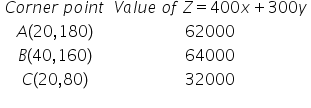
The maximum of the objective function is 64000 and it attains at A(40,160).
That is 40 first class tickets and 160 economy class tickets must be sold to get the maximum profit.
Answered by | 31 Jul, 2016, 21:21: PM
Concept Videos
CBSE 12-science - Maths
Asked by gargisha381 | 26 May, 2022, 12:24: PM
CBSE 12-science - Maths
Asked by ABHILASHA | 20 Apr, 2021, 12:07: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 22 Sep, 2014, 10:45: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 12 Sep, 2014, 15:47: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 31 Jul, 2016, 19:21: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 31 Jul, 2016, 18:04: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 31 Jul, 2016, 17:58: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 31 Jul, 2016, 17:47: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 31 Jul, 2016, 20:05: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM