CBSE Class 12-science Answered
A manufacturer can be exhibited diagrammatically as shown in fig
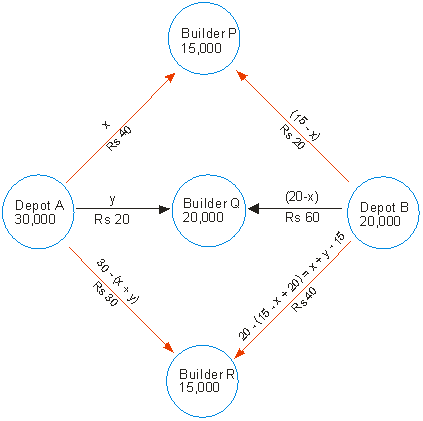
Let the depot A transport x thousands bricks to builders P, y thousands to builder Q. Since the depot A has stock of 30,000 bricks. Therefore, the remaining bricks i.e., 30-(x + y) thousands bricks will be transported to the builder R.
Since the number of bricks is always a non-negative real number.
Therefore,
x > 0, y > 0 and 30 - (x + y) > 0 ![]() x > 0, y > 0 and x + y < 30
x > 0, y > 0 and x + y < 30
Now, the requirement of the builder P is of 15000 bricks and x thousand bricks are transported from the depot A. therefore, the remaining (15 - x) thousands bricks are to be transported from the depot at B. The requirement of the builder Q is of 20,000 bricks and y thousand bricks are transported from depot A. Therefore, the remaining (20 - y) thousand bricks are to be transported from depot B.
Now, depot B has 20 - (15 - x + 20 - y) = x + y - 15 thousand bricks which are to be transported to the builder R.
Also, 15 - x > 0, 20 - y > 0 and x + y - 15 > 0
![]() x < 15, y < 20 and x + y > 15
x < 15, y < 20 and x + y > 15
The transportation cost from the depot A to the builders P, Q and R are respectively Rs 40x, 20y and
(30 - x - y). Similarly, the transportation cost from the depot B to the builders P, Q and R are respectively Rs 20( 15 - x), 60(20 - y) and 40(x + y - 15) respectively. Therefore, the total transportation cost Z is given by
Z = 40x + 20y + 30(30 - x - y) + 20(15 - x) + 60(20 - y) + 40(x + y - 15)
![]() Z = 30x - 30y + 1800
Z = 30x - 30y + 1800
Hence, the above LPP can be stated mathematically as follows :
Find x and y in thousands which
Minimize Z = 30x - 30y + 1800
Subject to
x + y < 30
x < 15
y < 20
x + y > 15
and, x > 0, y > 0
To solve this LPP graphically, we first convert in equations into equations and then draw the corresponding lines. The feasible region of the LPP is shaded in Fig. 29.25. The coordinates of the corner points of the feasible region A2 PQ B3 B2 are A2 (15, 0) P (15, 15), Q (10, 20), B3 0, 20) and B2 (0, 15). These points have been obtained by solving the corresponding intersecting lines simultaneously.
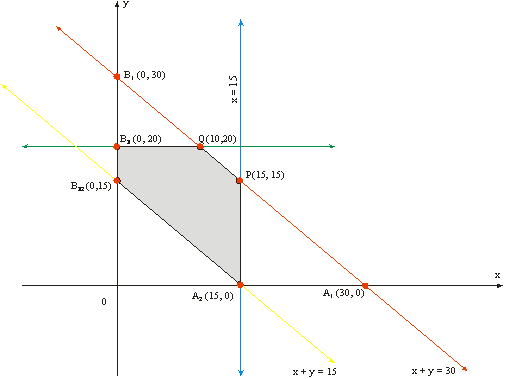
The value of the objective function at the corner points of the feasible region are given in the following table
|
Point (x, y) Value of the objective function X = 30x - 30y + 1800 |
|
A2 (15, 0) Z = 30 x 15 - 30 x 0 + 1800 = 2250 P (15, 15) Z = 30 x 15 - 30 x 15 + 1800 = 1800 Q (10, 20) Z = 30 x 10 - 30 x 20 + 1800 =1500 B2 (0, 15) Z = 30 x 0 - 30 x 15 + 1800 = 1350 |
Clearly, Z is minimum at x = 0, y = 20 and the minimum value Z is 1200.
Thus, the manufacturer should supply 0, 20 and 10 thousand bricks to builders P, Q and R from depot A and 15, 0 and 5 thousand bricks to builders P, Q and R from depot B respectively. In this case the minimum transportation cost will be Rs 1200