CBSE Class 9 Answered
The water drop falls at regular intervals from a tap 9 m above the ground. The fourth drop is leaving the tap at the instant, the first drop touches the ground. How high is the third drop at that instant?
Asked by anujha54 | 13 May, 2021, 12:03: PM
Time taken t1 by first drop to travel through 9 m vertical distance is determined by the following equation
h1 = (1/2) g t12
where h1 = 9 m is vertical distance , g is acceleration due to gravity and t1 is time taken
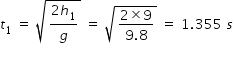
There are three equal intervals when four drops are falling from tap in this time t = 1.355 s
interval time = ( 1.355 / 3 ) = 0.452 s
Hence third drop has travelled one interval times , i.e., t3 = 0.452 s
Vertical distance travelled by third drop, h3 = (1/2) g t32 = 0.5 × 9.8 × 0.452 × 0.452 = 1 m
Hence third drop is at a height of 8 m above ground , when first drop has reached the ground
Answered by Thiyagarajan K | 13 May, 2021, 12:47: PM
Application Videos
Concept Videos
CBSE 9 - Physics
Asked by varshuparekh | 03 Jun, 2024, 18:34: PM
CBSE 9 - Physics
Asked by janhavisoni2099 | 02 Oct, 2023, 17:20: PM
CBSE 9 - Physics
Asked by sagrawal0081 | 18 Aug, 2023, 17:04: PM
CBSE 9 - Physics
Asked by ketkiparasgandhi | 05 Jul, 2023, 20:02: PM
CBSE 9 - Physics
Asked by adityatripathi84418 | 02 May, 2023, 22:29: PM
CBSE 9 - Physics
Asked by rsaranya658 | 30 Jun, 2022, 14:44: PM
CBSE 9 - Physics
Asked by poornimaram165 | 21 Jun, 2022, 21:16: PM
CBSE 9 - Physics
Asked by saanidhyapatil | 16 Feb, 2022, 13:23: PM
CBSE 9 - Physics
Asked by pradeepkumarbhegde5175 | 12 Jan, 2022, 23:25: PM