Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

Show that the function f (x) = x2 is strictly increasing function on [0,∞).
Asked by Topperlearning User | 06 Aug, 2014, 08:12: AM
answered-by-expert Expert Answer

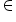Let x1, x2 element of[0,¥) such that x1 < x2. Then,

x1 < x2  => x12 < x1x2..........(i) [Multiplying both sides by x1]

and, x1 < x2  => x1x2<x22 ............ (ii) [Multiplying both sides by x2]

From (i) and (ii), we get

x1 < x2 => x12 < x22 => f (x1) < f (x2)

Thus, x1 < x2 => f (x1) < f (x2) for all x1, x2­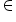 element of [0, ¥)

Hence, f (x) is strictly increasing function on [0, ¥)

Answered by | 06 Aug, 2014, 10:12: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 12-science - Maths
A man is moving away from a 40 m high tower at a speed of 2m/s . find the rate at which angle of elevation of the top of the tower  is changing when he is at a distance of 30m from foot of tower. Assume that eye level of the man is 1.6 m from the ground. explain in great detail
Asked by haroonrashidgkp | 08 Sep, 2018, 04:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Show that the function f (x) = 2x + 3 is strictly increasing function on R.
Asked by Topperlearning User | 06 Aug, 2014, 08:00: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Show that the function f (x) = x2 is strictly increasing function on [0,∞).
Asked by Topperlearning User | 06 Aug, 2014, 08:12: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Show that the function f (x) = ax, a > 1 is strictly increasing on R.
Asked by Topperlearning User | 06 Aug, 2014, 09:18: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the intervals in which f (x) = –x2 – 2x + 15 is increasing or decreasing
Asked by Topperlearning User | 06 Aug, 2014, 09:20: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the intervals in which the function f (x) is increasing, f (x) = 2x3 - 9x2 + 12x + 15
Asked by Topperlearning User | 06 Aug, 2014, 09:22: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the intervals in which the function f (x) is  decreasing f(x) = 2x3 + 9x2 + 12x + 20
Asked by Topperlearning User | 06 Aug, 2014, 09:29: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the intervals in which f (x) = (x + 1)3 (x - 3)3 is increasing or decreasing.
Asked by Topperlearning User | 06 Aug, 2014, 09:54: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Find the intervals in which the function f (x) = log left parenthesis 1 plus straight x right parenthesis minus fraction numerator 2 straight x over denominator 1 plus straight x end fraction is increasing or decreasing
Asked by Topperlearning User | 06 Aug, 2014, 10:12: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Maths
Determine the intervals in which the function f (x) = x4 – 8x3 + 22x2 – 24x + 21 is decreasing or increasing
Asked by Topperlearning User | 06 Aug, 2014, 10:17: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×