Ask a Doubt

Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

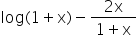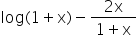Find the intervals in which the function f (x) = _{$log left parenthesis 1 plus straight x right parenthesis minus fraction numerator 2 straight x over denominator 1 plus straight x end fraction$} is increasing or decreasing

Asked by Topperlearning User | 06 Aug, 2014, 10:12: AM

Expert Answer

We have,

f (x) = $log left parenthesis 1 plus straight x right parenthesis minus fraction numerator 2 straight x over denominator 1 plus straight x end fraction$

Clearly, f (x) is defined for all x satisfying

x + 1 > 0 i.e. x > – 1

So, domain (f) = (–1, ¥)

Now,

f (x) = $log left parenthesis 1 plus straight x right parenthesis minus fraction numerator 2 straight x over denominator 1 plus straight x end fraction$

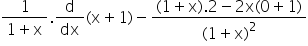
Þ f ¢ (x) = _{$fraction numerator 1 over denominator 1 plus straight x end fraction. straight d over dx left parenthesis straight x plus 1 right parenthesis minus fraction numerator left parenthesis 1 plus straight x right parenthesis.2 minus 2 straight x left parenthesis 0 plus 1 right parenthesis over denominator left parenthesis 1 plus straight x right parenthesis squared end fraction$}

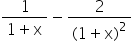
Þ f ¢ (x) = _{$fraction numerator 1 over denominator 1 plus straight x end fraction minus fraction numerator 2 over denominator left parenthesis 1 plus straight x right parenthesis squared end fraction$}

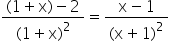
Þ f ¢ (x) = _{$fraction numerator left parenthesis 1 plus straight x right parenthesis minus 2 over denominator left parenthesis 1 plus straight x right parenthesis squared end fraction equals fraction numerator straight x minus 1 over denominator left parenthesis straight x plus 1 right parenthesis squared end fraction$}

For f (x) is be increasing, we must have

f¢ (x) > 0

Þ 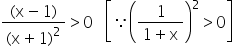$fraction numerator left parenthesis straight x minus 1 right parenthesis over denominator left parenthesis straight x plus 1 right parenthesis squared end fraction greater than 0 space space space open square brackets because open parentheses fraction numerator 1 over denominator 1 plus straight x end fraction close parentheses squared greater than 0 close square brackets$

Þ x - 1 > 0

Þ x > 1

Þ x Î (1, ¥)

So, f (x) is increasing on (1, ¥)

Hence, f (x) is increasing in its domain

Answered by | 06 Aug, 2014, 12:12: PM

Concept Videos

Practice Test

Pre Board Assessment

Answered Unanswered My Questions My Answers

CBSE 12-science - Maths

A man is moving away from a 40 m high tower at a speed of 2m/s . find the rate at which angle of elevation of the top of the tower is changing when he is at a distance of 30m from foot of tower. Assume that eye level of the man is 1.6 m from the ground. explain in great detail

Asked by haroonrashidgkp | 08 Sep, 2018, 04:16: PM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Show that the function f (x) = 2x + 3 is strictly increasing function on R.

Asked by Topperlearning User | 06 Aug, 2014, 08:00: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Show that the function f (x) = x² is strictly increasing function on [0,∞).

Asked by Topperlearning User | 06 Aug, 2014, 08:12: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Show that the function f (x) = a^x, a > 1 is strictly increasing on R.

Asked by Topperlearning User | 06 Aug, 2014, 09:18: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the intervals in which f (x) = –x² – 2x + 15 is increasing or decreasing

Asked by Topperlearning User | 06 Aug, 2014, 09:20: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the intervals in which the function f (x) is increasing, f (x) = 2x³ - 9x² + 12x + 15

Asked by Topperlearning User | 06 Aug, 2014, 09:22: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the intervals in which the function f (x) is decreasing f(x) = 2x³ + 9x² + 12x + 20

Asked by Topperlearning User | 06 Aug, 2014, 09:29: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the intervals in which f (x) = (x + 1)³ (x - 3)³ is increasing or decreasing.

Asked by Topperlearning User | 06 Aug, 2014, 09:54: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Find the intervals in which the function f (x) = _{$log left parenthesis 1 plus straight x right parenthesis minus fraction numerator 2 straight x over denominator 1 plus straight x end fraction$} is increasing or decreasing

Asked by Topperlearning User | 06 Aug, 2014, 10:12: AM

ANSWERED BY EXPERT

CBSE 12-science - Maths

Determine the intervals in which the function f (x) = x⁴ – 8x³ + 22x² – 24x + 21 is decreasing or increasing

Asked by Topperlearning User | 06 Aug, 2014, 10:17: AM

ANSWERED BY EXPERT

My Class Videos Tests Plans Ask a Doubt