CBSE Class 12-science Answered
Show that the function f (x) = ax, a > 1 is strictly increasing on R.
Asked by Topperlearning User | 06 Aug, 2014, 09:18: AM
Let x1, x2 Î R such that x1 < x2. Then,
x1 < x2
=> ax1 < ax2 [Since a>1 also, x1>x2 =>ax1 > ax2]
=> f (x1) < f (x2)
Thus, x1, x2 Þ f(x1) < f(x2) for all x1, x2 Î R
Hence, f (x) is strictly increasing function on R
Answered by | 06 Aug, 2014, 11:18: AM
Concept Videos
CBSE 12-science - Maths
Asked by haroonrashidgkp | 08 Sep, 2018, 04:16: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 08:00: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 08:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:18: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:20: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:22: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:29: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:54: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 10:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 10:17: AM




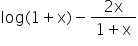 is increasing or decreasing
is increasing or decreasing