CBSE Class 12-science Answered
Find the intervals in which the function f (x) is decreasing f(x) = 2x3 + 9x2 + 12x + 20
Asked by Topperlearning User | 06 Aug, 2014, 09:29: AM
We have,
f (x) = 2x3 + 9x2 + 12x + 20
\ f ' (x) = 6x2 + 18x + 12 = 6(x2 + 3x + 2)
(i) for f (x) to be increasing, we must have
f ' (x) > 0
=> 6(x2 + 3x + 2) > 0
=> (x2 + 3x + 2) > 0 [![]() 6 > 0 and 6 (x2 + 3x + 2) > 0 \ x2 + 3x + 2 > 0]
6 > 0 and 6 (x2 + 3x + 2) > 0 \ x2 + 3x + 2 > 0]
=> (x + 1) (x + 2) > 0
=> x < -2 or x > -1
Therefore, (-¥, -2) & (-1, ¥)
So, f (x) is increasing on (¥, -2) & (-1, ¥)
(ii) for f (x) to be decreasing, we must have
f ' (x) < 0
=> 6(x2 + 3x + 2) < 0
=> x2 + 3x + 2 < 0 [![]() 6 > 0 and 6(x2 + 3x + 2) < 0 \ x2 + 3x + 2 < 0]
6 > 0 and 6(x2 + 3x + 2) < 0 \ x2 + 3x + 2 < 0]
=> (x + 1)(x + 2) < 0
-2 < x < -1
So, f (x) is decreasing on (-2, -1)
Answered by | 06 Aug, 2014, 11:29: AM
Concept Videos
CBSE 12-science - Maths
Asked by haroonrashidgkp | 08 Sep, 2018, 16:16: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 08:00: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 08:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:18: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:20: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:22: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:29: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:54: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 10:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 10:17: AM




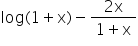 is increasing or decreasing
is increasing or decreasing