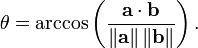CBSE Class 11-science Answered
PROVE THAT SCALAR PRODUCT OF 2 PERPENDICULAR VECTORS IS ZERO
Asked by rksvikhyat | 01 Jun, 2012, 09:39: AM
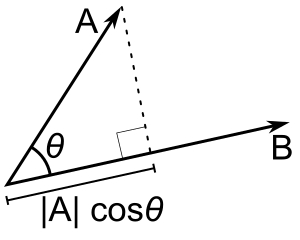
In Euclidean geometry, the dot product of vectors expressed in an orthonormal basis is related to their length and angle. For such a vector  , the dot product
, the dot product  is the square of the length (magnitude) of
is the square of the length (magnitude) of  , denoted by
, denoted by  :
:
If  is another such vector, and
is another such vector, and 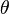 is the angle between them:
is the angle between them:
This formula can be rearranged to determine the size of the angle between two nonzero vectors:
The CauchySchwarz inequality guarantees that the argument of  is valid.
is valid.
One can also first convert the vectors to unit vectors by dividing by their magnitude:
then the angle 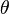 is given by
is given by
Answered by | 01 Jun, 2012, 09:49: AM
Concept Videos
CBSE 11-science - Physics
Asked by roshnibudhrani88 | 23 Mar, 2024, 05:52: PM
CBSE 11-science - Physics
Asked by vinitdubey7735 | 14 Mar, 2024, 11:21: AM
CBSE 11-science - Physics
Asked by shailajakandikatla19 | 18 Jan, 2024, 06:40: PM
CBSE 11-science - Physics
Asked by dhanshreekansyakar | 09 Jan, 2024, 11:57: AM
CBSE 11-science - Physics
Asked by banhisikhapanda49 | 07 Nov, 2023, 10:42: PM
CBSE 11-science - Physics
in a vertical circle of radius r at what point in its path a particle may have tension equal to zero
Asked by momintaufik26 | 13 Oct, 2023, 08:26: PM
CBSE 11-science - Physics
Asked by anshujaiswalname | 10 Sep, 2023, 01:29: PM
CBSE 11-science - Physics
Asked by subhashreeojha235 | 20 Jul, 2023, 11:22: AM
CBSE 11-science - Physics
Asked by preethiprithivi05 | 21 Feb, 2023, 09:28: PM
CBSE 11-science - Physics
Asked by hy9022075 | 11 Jan, 2023, 05:06: PM