CBSE Class 11-science Answered
PLEASE TELL ME HOW TO DERIVE THE FORMULA FOR AREA OF A CIRCLE USING BOTH DIFFERENTIAL AND INTEGRAL CALCULUS.
Asked by kandappan | 25 Sep, 2019, 10:12: AM
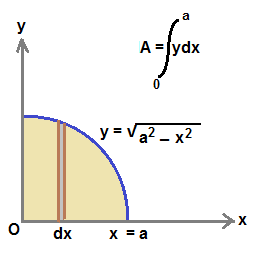
By integration:-
Area of the circle is obtained by finding the area A under curve whose equation is y = (a2 - x2 )1/2 , where a is radius of circle.
Area of circle is four times of A.
Let us consider a strip of width dx. Area of this strip is ( y dx ).
Area A is obtained by summing the area dA of such strip from x=0 to x=a.
Hence
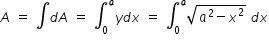
Above intergration is performed by using substitution x = a sinθ.
By integration we get, A = (π/4)a2
Hence area of circle = 4 A = πa2 Sq. Units
-------------------------------------------------------------------------
Integration is nothing but continuous sum.
Hence area is considered as summation of small area elements that form the circle area and area is calculated by integration.
Differentiation is change in function for a small change of function variable.
It is not possible to find a method of finding area of circle by differentiation
Answered by Thiyagarajan K | 25 Sep, 2019, 12:24: PM
CBSE 11-science - Physics
Asked by sheikhsaadat24 | 17 Apr, 2024, 09:41: PM
CBSE 11-science - Physics
Asked by sy123946 | 07 Apr, 2024, 04:23: PM
CBSE 11-science - Physics
Asked by derhebha955 | 03 Apr, 2024, 09:03: AM
CBSE 11-science - Physics
Asked by sumedhasingh238 | 29 Mar, 2024, 05:15: PM
CBSE 11-science - Physics
Asked by sumedhasingh238 | 28 Mar, 2024, 11:10: PM
CBSE 11-science - Physics
Asked by roshnibudhrani88 | 23 Mar, 2024, 05:52: PM
CBSE 11-science - Physics
Asked by emad.amd | 21 Mar, 2024, 12:00: PM
CBSE 11-science - Physics
Asked by vinitdubey7735 | 14 Mar, 2024, 11:21: AM
CBSE 11-science - Physics
Asked by om636694 | 04 Mar, 2024, 09:10: PM
CBSE 11-science - Physics
Asked by rajuinwati12 | 04 Mar, 2024, 09:22: AM




