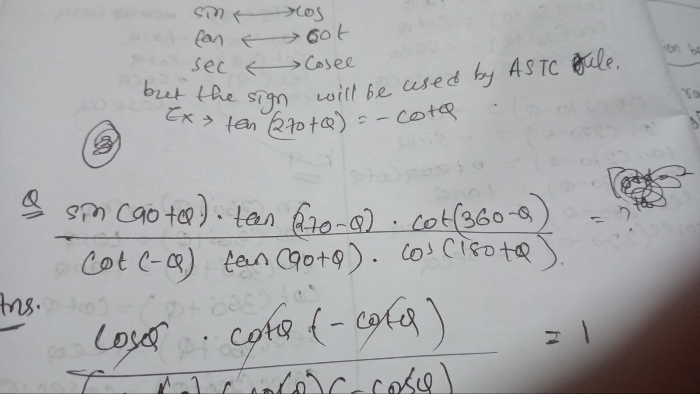CBSE Class 11-science Answered
no. of solution of the equation are?
Asked by | 13 Nov, 2012, 02:06: PM
Expert Answer
We know that asin?+bcos?=?a^2+b^2 sin(?+A) where cos A=a/?a^2+b^2
Therefore, we have:
(?3)sinx + cosx) =2 sin(x+?/6)
And (?3)sin2x - cos2x) = 2 sin (2x-?/6)
And so
|
{(?3)sinx + cosx }t=4 where t = ? {(?3)sin2x - cos2x + 2} |
Can be written as 2^t sin(x+?/6)^t=2^2
Where t=?2sin(2x-?/6)+2
This equation will have solution only when both sin(x+?/6) andsin(2x-?/6) will be one so that t=2and as this is possible for x=?/3,and sinx and sin2x both will be having common period of 2?leanth,solution will repeat after a length of 2? .so there will be infinite solutions.
Answered by | 20 Nov, 2012, 12:50: PM
Concept Videos
-
Trigonometric identities and problems
Fundamental trigonometric identities and problems based on them. Sign Conve... -
Degree measure and Radian measure ...
This video explains the concept of negative & positive angles, conversion o... -
Domain, period and range of trigonometric functions ...
Define the domain, period and range of the trigonometric functions and plot... -
Basic Trigonometric Formulae
Derive and apply the basic formulae of sine and cosine functions like sin(... -
Sign of Trigonometric Functions
This video covers values of trigonometric ratios of angles greater than 90 ...
CBSE 11-science - Maths
Asked by rajyothi64 | 05 Mar, 2024, 09:49: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by ghoshshawata62 | 04 Mar, 2024, 08:16: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by nayaktapaswini2007 | 29 Feb, 2024, 09:10: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by bimanmandal53361 | 15 Jan, 2024, 12:32: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by sreyas.katuri | 23 Sep, 2023, 07:12: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by 069.pks | 16 Sep, 2023, 10:06: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by surekhashriwas01 | 12 Sep, 2023, 08:39: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by mvr23467 | 12 Sep, 2023, 07:52: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by SasipriyaNagappan | 27 Jul, 2023, 07:22: PM
ANSWERED BY EXPERT
