Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 12-science Answered

In a FCC lattice , atoms A occupy the corner positions and atoms B occupy the face centre positions. If one atom of B is missing from one of the face centred points, calculate the formula of the compound
Asked by akash9322793205 | 12 Aug, 2021, 09:30: AM
answered-by-expert Expert Answer
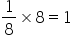
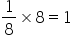
In a face centered cubic lattice, atom (A) occupies the corner positions. There are 8 corner positions and each position contributes one eighth to the unit cell. Hence, total number of (A) atoms per unit cell= 1 over 8 cross times 8 equals 1


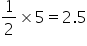
Atom (B) occupied the face centre positions. There are six face centre positions. One atom of (B) is missing from one of the face centered points. Thus, there are 5 face centre positions that are occupied with (B). Each such position contributes one half to the unit cell. Hence, total number of (B) atoms per unit cell.= 1 half cross times 5 equals 2.5

The formula of the compound is AB2.5 
                                               A2 B5
Answered by Ravi | 12 Aug, 2021, 12:01: PM

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 12-science - Chemistry
In a FCC lattice , atoms A occupy the corner positions and atoms B occupy the face centre positions. If one atom of B is missing from one of the face centred points, calculate the formula of the compound
Asked by akash9322793205 | 12 Aug, 2021, 09:30: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
  What is the formula of a compound in which the element Y forms hcp lattice and atoms of X occupy 2/3rdof tetrahedral voids
Asked by thakurranjan54 | 08 Feb, 2021, 06:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
what is the lattice parameter of GaAs? radius of Ga=122 pm, As=125 pm
Asked by sildasholly2002 | 26 Jul, 2020, 06:37: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
an fcc lattice has lattice parameters a=400 pm . calculate the molar volume of the lattice including all the empty space
Asked by tejuaaygole | 11 Jul, 2020, 10:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
each edge of a cubic unit cell is 400 pm long. if atomic weight of the element is 120 and its density is 6.25 g/cm3. The crystal lattice is : a) simple cubic   b)BCC c) FCC                c) NONE
Asked by chandlerbong164 | 12 Apr, 2020, 07:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
What is a unit cell? Explain bravais lattices  
Asked by mangeshkale423 | 25 Feb, 2020, 05:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
What is the formula of a compound in which the element Y forms hcp lattice and atoms of X occupy 2/3rd of tetrahedral voids
Asked by upasana.sobti | 16 Jan, 2019, 01:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
CBSEXII| CHEMISTRYMOST IMPORTANT QUESTIONSwww.topperlearning.com2CBSEClass XII ChemistryMost Important QuestionsChapter 1: The Solid State1.What is the formula of a compound in which the element Y forms hcp lattice and atoms of X occupy 2/3rdof tetrahedral voids?[1M]2.Givean example each of a molecular solid and an ionic solid.[1M]3.An element with density 2.8gcm-3forms a fccunit cellwith edgelength 4 × l0-8cm. Calculate the molar mass of the element.[2M](Given: NA=6.022 × 1023mol-1)4.[2M](i)What type of non-stoichiometric point defect is responsible for the pink colour of LiCl?(ii)What type of stoichiometric defect is shown by NaCl? 5.How will you distinguish between the following pairs of terms?[2M](i)Tetrahedral and octahedral voids(ii)Crystal lattice and unit cell 6.Tungsten crystallizes in body centred cubic unit cell. If the edge of the unit cell is 315.5pm, what is the radius of tungsten atom? [3M]7.Iron has a body centred cubic unit cell with a cell dimension of 286.65 pm,the density of iron is 7.874 gcm-3. Use this information to calculate Avogadro's number. (At.Mass of Fe = 55.845 μ).[3M]8.An element with density 10 gcm−3forms a cubic unit cell with edge length of 3 × 10−8cm. What is the nature of the cubic unit cell if the atomic mass of the element is 81 gmol−1? [3M] CBSEXII| CHEMISTRYMOST IMPORTANT QUESTIONSwww.topperlearning.com39.(a)An element has a body centered cubic structure with a cell edge of 288 pm. Thedensity of the elements is 7.2 gcm-3. Calculate the number of atoms present is 208 g of the element.[3M](b) With example explain difference between crystalline and amorphous solids. [2M]Chapter 2: Solutions1.A 1.00 molal aqueous solution of trichloroacetic acid (CCl3COOH) is heated to its boiling point. The solution has the boiling
Asked by Harsh.1102.raj | 10 Jan, 2019, 09:23: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
An element X' (At. mass a 40 g mol-1) having f.c.c. structure, has unit cell edge length of 400 pm. Calculate the density of ‘X’ and the number of unit cells in 4 g of ‘X’. (NA = 6.022 x 1023 mol-1)
Asked by raul.chintakindi14 | 14 Mar, 2018, 11:44: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 12-science - Chemistry
What is the volume occupied in body centered cube.
Asked by Topperlearning User | 16 Jun, 2016, 03:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt

Be a Top Scorer in the Exam with Test Series and Test Generator!

Enrol Now
×