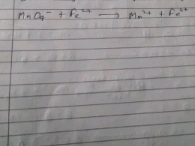CBSE Class 11-science Answered

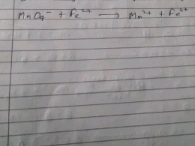
Step 1: Write down the chemical reaction's skeleton equation. All reactants and by-products must be identified. Write the reaction in ionic form for a better result.

 NO₃⁻ + I₂ → IO₃⁻ + NO₂

Step 2: Divide the process into two halves. A redox reaction is the simultaneous occurrence of oxidation and reduction reactions.

a) Each atom in the equation should be assigned an oxidation number. The oxidation number (also known as the oxidation state) of an atom in a chemical is a measure of its degree of oxidation.

(N⁺⁵O⁻²₃)⁻ + I⁰₂ → (I⁺⁵O₃⁻²)⁻ + N⁺⁴O⁻²₂

b) Identify and write down all of the redox couples in the reaction. Determine which reactants are oxidised (the oxidation number rises when they react) and which are reduced (the oxidation number falls). Make a note of the electron transfer. Insert coefficients as needed to make the numbers of oxidised and reduced atoms on the two sides of each redox pair equal.

Oxidtion of I : I₂⁰ → (2I⁺⁵O⁻²₃)⁻ + 10e⁻ 

Reduction of N : (N⁺⁵O⁻²₃)⁻ + e⁻ → N⁺⁴O⁻²₂

c) Combining these redox couples results in two half-reactions: one for oxidation and one for reduction.

Oxidation :  I₂⁰ → (2I⁺⁵O₃⁻²)⁻ + 10e⁻

Reduction: (N⁺⁵O₃⁻²)⁻ + e⁻ → N⁺⁴O₂⁻²

Step 3: Balance the atoms in each half-reaction. A chemical equation must have the same number of atoms of each element on both sides of the equation. Add appropriate stoichiometric coefficients in front of the chemical formulas to balance the number of atoms. Never change any formulas.

a) Balance all other atoms except hydrogen and oxygen. We can use any of the species that appear in the skeleton equations for this purpose. Keep in mind that reactants should be added only to the left side of the equation and products to the right.

Oxidation: I⁰₂ → (2I⁺⁵O₃⁻²)⁻ + 10e⁻

Reduction: (N⁺⁵O₃^-2) ⁻ + e⁻ → N⁺⁴O₂⁻²

b) Balance the charge. For reactions in an acidic solution, balance the charge so that both sides have the same total charge by adding an H⁺ ion to the side deficient in positive charge.

Oxidation: I⁰₂ → (2I⁺⁵O⁻²₃)⁻ + 10e⁻ + 12H⁺

Reduction: N⁺⁵O⁻²₃⁻ + e⁻ + 2H⁺ → N⁺⁴O⁻²₂

c) The oxygen atoms must be balanced. Check to see if the left and right sides have the same number of oxygen atoms; if not, equilibrate these atoms by adding water molecules.

Oxidation: I⁰₂ + 6H₂O → (2I⁺⁵O₃⁻²)⁻ + 10e⁻ + 12H⁺

Reduction: (N⁺⁵O₃⁻²)⁻ + e⁻ + 2H⁺ → N⁺⁴O⁻²₂ + H₂O

Step 4. Equivalently, equalizes electron gain and loss. The electrons gained during the reduction half-reaction must equal those lost during the oxidation half-reaction. Multiply the coefficients of each species by the lowest common multiple of the half-reactions to make the two equal.

Oxidation: [I⁰₂ + 6H₂O → 2I⁺⁵O⁻²₃⁻ + 10e⁻ + 12H⁺] ⨯1

Reduction: [N⁺⁵O⁻²₃⁻ + e⁻ + 2H⁺ → N⁺⁴O⁻²₂ + H₂O] ⨯10

Thus,

Oxidation: I⁰₂ + 6H₂O → 2I⁺⁵O⁻²₃⁻ + 10e⁻ + 12H⁺

Reduction: 10N⁺⁵O⁻²₃⁻ + 10e⁻ + 20H⁺ → 10N⁺⁴O⁻²₂ + 10H₂O

Step 5. Combine the half-reactions. The two half-reactions can be merged in the same way as two algebraic equations can, with the arrow acting as an equals sign. Recombine the two half-reactions by combining all of the reactants on one side and all of the products on the other.

I⁰₂ + 10N⁺⁵O⁻²₃⁻ + 6H₂O + 10e⁻ + 20H⁺ → 2I⁺⁵O⁻²₃⁻ + 10N⁺⁴O⁻²₂ + 10e⁻ + 10H₂O + 12H⁺

Step 6. Simplify the equation. The same species on opposite sides of the arrow can be cancelled. Write the equation so that the coefficients are the smallest set of integers possible.

I⁰₂ + 10N⁺⁵O⁻²₃⁻ + 8H⁺ → 2I⁺⁵O⁻²₃⁻ + 10N⁺⁴O⁻²₂ + 4H₂O

Finally, always double-check if the equation is balanced. First, ensure that both sides of the equation have the same kind and number of atoms.

 Also ensure that the total of the charges on one side of the equation equals the total of the charges on the other. It makes no difference what the charge is as long as it is consistent on both sides.

1 ⨯ 0 + 10 ⨯−1 + 8 ⨯ 1 = 2 ⨯ −1 + 10 ⨯ 0 + 4 ⨯ 0

−2 = −2

We can create a balanced equation because the sum of individual atoms on the left side of the equation equals the sum of the same atoms on the right side, and because the charges on both sides are equal.