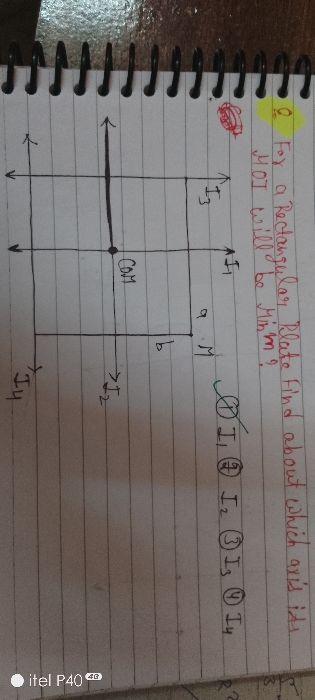
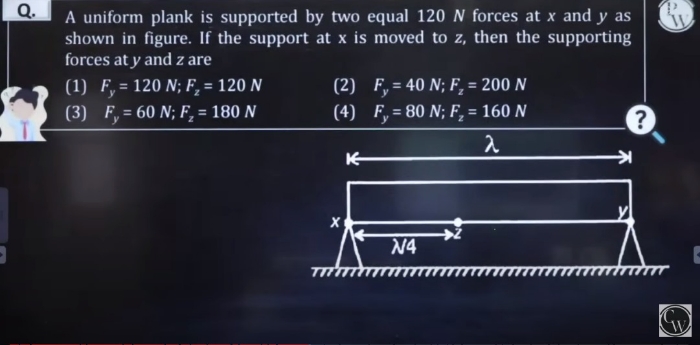
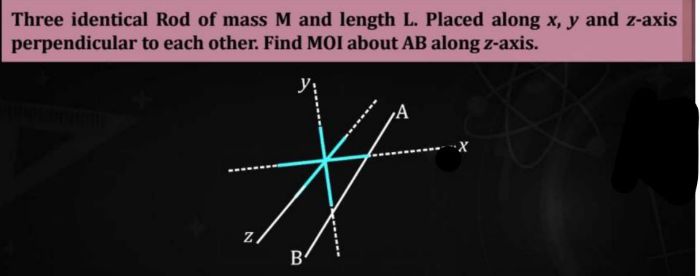
NEET Class neet Answered
How to solve this question?
Asked by anshadali111 | 07 May, 2021, 04:08: PM
Expert Answer
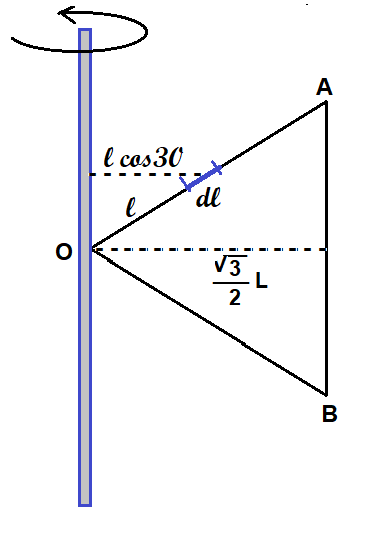
Figure shows an equilateral triangle OAB and axis of rotation passes through a corner O.
Moment of inertia I of system about the given axis of rotation is given as
I = IAB + IOA + IOB
Where IAB Is moment of inertia of rod AB . Similarly moment of inertia of other two rods are considered.
Since thin rod AB is symmetrically placed about axis of rotation, we have
IAB = M × [ ( √3 /2 ) L ]2 = (3/4) M L2
Moment of inertia IOA of rod OA is determined as follows
Let ρ be the linear density of rod , ρ = ( M / L ) .
Let us consider small element of length dl in the rod at a distaance l along the rod from O as shown in figure.
Moment of inertia dI of this small element , dI = dm (l cos30)2 .
Moment of inertia of rod of full length OA is determined as
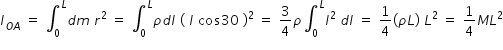
Similarly we get , IOB = (1/4) M L2
I = IAB + IOA + IOB = M L2 [ (3/4) + (1/4) + (1/4) ] = (5/4) M L2
Answered by Thiyagarajan K | 07 May, 2021, 06:18: PM
NEET neet - Physics
Asked by meheboob1doctor | 21 Dec, 2022, 09:09: AM
ANSWERED BY EXPERTNEET neet - Physics
Asked by meheboob1doctor | 20 Dec, 2022, 11:11: AM
ANSWERED BY EXPERTNEET neet - Physics
Asked by yohanagrawal | 15 Jul, 2022, 12:43: AM
ANSWERED BY EXPERTNEET neet - Physics
Asked by reshmitag04 | 07 Jun, 2022, 06:41: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by anshikabhardwaj272003 | 23 Jan, 2022, 04:56: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by jhajuhi19 | 07 Sep, 2021, 06:59: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by ayush.gupta3052 | 10 Jul, 2021, 07:01: PM
ANSWERED BY EXPERTNEET neet - Physics
Asked by aniketchalak145 | 09 Jul, 2021, 07:58: AM
ANSWERED BY EXPERTNEET neet - Physics
Asked by anshadali111 | 07 May, 2021, 04:08: PM
ANSWERED BY EXPERT