CBSE Class 12-science Answered
Help in this question.
Asked by carnivalgirl8421 | 29 Jun, 2022, 10:06: PM
Expert Answer
Total Flux Φ of electric field passing through the surface of cone is given as
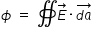........................... (1)where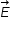 
is intensity of electric field at surface of cone and 
is small area element on the surface of cone.
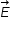is intensity of electric field at surface of cone and is small area element on the surface of cone.Above equation implies that intensity of electric frield is integrated over the closed surface of cone.
By Gauss theorem, we have
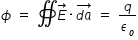........................... (2)where q is enclosed charge inside the volume of cone.
In this case, enclosed charge is zero , because we are given that electric field intensity is 20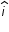
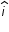N/C .
N/C .Given electric field intensity is uniform and directed along x-axis.
We will not get such a uniform intensity of electric field over the surface of cone
if there is an enclosed charge within the volume of cone.
Hence from eqn.(2) and by knowing that enclosed charge is zero ,
it can be concluded that total flux of electric field through the surface of cone is zero.
Physically we can infer that whatever flux entering from left side surface of cone is leaving
through right side surface of cone so that total flux of electric field over the surface of cone is zero.
Answered by Thiyagarajan K | 30 Jun, 2022, 08:08: AM
Concept Videos
CBSE 12-science - Physics
Asked by hussain221man | 05 Apr, 2024, 08:44: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by am1954077 | 08 Mar, 2024, 04:57: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by carnivalgirl8421 | 29 Jun, 2022, 10:06: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by hitanshu04 | 27 May, 2021, 07:33: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by hitanshu04 | 22 May, 2021, 07:41: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by jayasartasarta995 | 09 May, 2021, 10:32: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by dasdebasish25082003 | 22 Aug, 2020, 06:01: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by mddanis71895 | 21 Aug, 2020, 06:45: PM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by shitikanthdas31 | 15 Jun, 2019, 09:58: AM
ANSWERED BY EXPERTCBSE 12-science - Physics
Asked by dharaelect | 27 Mar, 2019, 10:28: PM
ANSWERED BY EXPERT
