Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

ICSE Class 10 Answered

from the top of a hill the angle of depression of two consecutive kilometre stones due east are found to be 30 degrees ahd 45 degrees respectively. find the distance of the two stones from the foot of the hill.
Asked by pradipdhole | 17 Jun, 2019, 19:39: PM
answered-by-expert Expert Answer
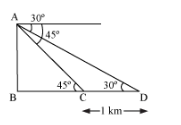
AB is the hill. Point C and D are the positions of the stones on the ground such that CD = 1 km
In ΔABC 
AB/BC = tan 45°
AB/BC = 1
BC = AB ....(i)
In ΔABD 
AB/BD = tan 30°
AB/BD = 1/√3
BD = √3 AB ....(ii)
CD = 1 km
BD - BC = 1 km
√3 AB - AB = 1
(√3 - 1)AB = 1
AB = 1/(√3 - 1)
AB = (√3 + 1)/2 km
Hence, the height of the hill is (√3 + 1)/2 km
Answered by Sneha shidid | 18 Jun, 2019, 09:45: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
ICSE 10 - Maths
The angle of elevation of a bird from a point 50 m above the lake is 30(Degree) and the angle of depression of its reflection in the lake is 60(Degree). find the height of the bird above the lake. With the diagram
Asked by san.dhole121409 | 09 Feb, 2024, 00:25: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
can u ppls explain heights and distNces   
Asked by gvsaishruthi | 05 Mar, 2021, 21:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
From the top of a cliff, 50m high, the angle of depression of a buoy is 30 degree . Calculate to the nearest meter , the distance of the buoy from the foot of the cliff  
Asked by maitripatel9069.10sdatl | 11 May, 2020, 18:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
Can anyone please answer question c  
question image
Asked by geetajsr765 | 25 Mar, 2020, 18:43: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
The upperpart of tree broken by the wind makes an angle of 45 with the ground and distance from the root to point where the top of the tree touches the ground is 15 m what was the ht of the tree before it was broken  
Asked by anwarenr | 30 Nov, 2019, 13:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
Two people standing on the same side of a tower in a straight line with it, measure the angles of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m, find the distance between the two people.
Asked by venkatesh.keshavamurthy | 16 Aug, 2019, 23:42: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
from the top of a hill the angle of depression of two consecutive kilometre stones due east are found to be 30 degrees ahd 45 degrees respectively. find the distance of the two stones from the foot of the hill.
Asked by pradipdhole | 17 Jun, 2019, 19:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
an aeroplane at an altitude of 250m observes the angle of depression of two boats on opposite banks of a river to be 45 degree and 60 degree respectively find width of river(please include diagram and explaination to each step)
Asked by ushanihar12 | 04 Feb, 2019, 21:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
a man on the bank of a stream observes a tree on the opposite bank exactly across the stream he finds the angle of elevation of the top of the tree to be 45. on receding perpendicularly a distance of 4m from the bank, he finds that the angle of elevation reduces by 15 .is this information sufficient for the man to determine the height of the tree and the width of the stream? if so, find them.    heights and distance
Asked by triptisrivastava2002 | 14 Oct, 2018, 15:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
The shadow of a tower standing on a level ground is found to be 61.59m longer. When the sun altitudes 34°30`then when it is 50°.find the height of the tower.
Asked by priya_dsl | 13 Sep, 2018, 22:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt