Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

ICSE Class 10 Answered

FIND THE SUM OF ALL  ODD NO. LESS THAT 50 AND FIRST 12 NATURAL NUMBERS EACH OF WHICH IS A MULTIPAL OF 7  
Asked by atanvi2006 | 22 May, 2021, 01:41: PM
answered-by-expert Expert Answer
The first odd number is 1 and the last odd number is 49
The numbers 1, 3, 5, 7, ..., 49 forms an A.P. with a = 1 and d = 2
Let an = 49
a + (n - 1)d = 49
1 + (n - 1)2 = 49
Therefore, n = 25
Sum of n odd numbers is n2 
Therefore, sum of odd numbers less than 50 is 252 = 625
 
 
First 12 multiples of 7 are 7, 14, 21, ..., 84
This forms an A.P. with a = 7 and d = 7
Sum of n terms of an A.P. is given by
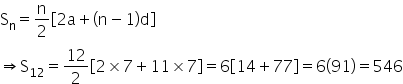
straight S subscript straight n equals straight n over 2 open square brackets 2 straight a plus open parentheses straight n minus 1 close parentheses straight d close square brackets rightwards double arrow straight S subscript 12 equals 12 over 2 open square brackets 2 cross times 7 plus 11 cross times 7 close square brackets equals 6 open square brackets 14 plus 77 close square brackets equals 6 open parentheses 91 close parentheses equals 546
Answered by Renu Varma | 25 May, 2021, 11:42: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
ICSE 10 - Maths
An AP 5,12,19,...has 50 terms.find its last term  
Asked by dr904265 | 26 Sep, 2022, 09:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
The sum of the first six terms of an A.P is 42. The ration of the 10th and 30th term is 1:3. Find the first and 13th term.
Asked by srivastavasrishti454 | 13 Sep, 2021, 08:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
FIND THE SUM OF ALL  ODD NO. LESS THAT 50 AND FIRST 12 NATURAL NUMBERS EACH OF WHICH IS A MULTIPAL OF 7  
Asked by atanvi2006 | 22 May, 2021, 01:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
Find the number of terms: 5 2 -1 ......-49
Asked by bhavishgowdabs355 | 30 Apr, 2021, 09:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
Determine the A.P., whose fifth term is 16 and the difference of the eighth term from the thirteenth term is 20.
Asked by 4321sandeep | 11 Oct, 2020, 11:46: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
10the term of the sequence tn=2n-5
Asked by shobhamgowda179 | 15 Sep, 2020, 08:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
The first term of two A.P.s are equal and the ratios of their common differences is 1:2 If the 7th term of first A.P and 21th term of second A.P are 23 and 125 respectively. Find two A.P.s
Asked by www.maniyarsufiyan13 | 26 Jun, 2020, 12:19: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
How to find nth term of an arithematic sequences
Asked by Www.shazils123 | 10 Jul, 2019, 08:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
Can 2n² -7 be the n th term of an A.P.?Explain.
Asked by krcraju1973 | 10 Jun, 2019, 09:43: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
If the n th term of the A.P .58,60,63........  is equal to the n th term of the A.P -2,5,12.......,find the value on n.
Asked by krcraju1973 | 09 Jun, 2019, 05:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×