CBSE Class 12-science Answered
find the area of the triangle formed by the line x + y = 3 and angle bisectors of the pair of straight lines 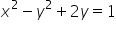 .
.
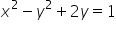 .
.
Asked by Topperlearning User | 12 Aug, 2016, 23:48: PM
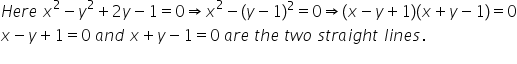 .
.
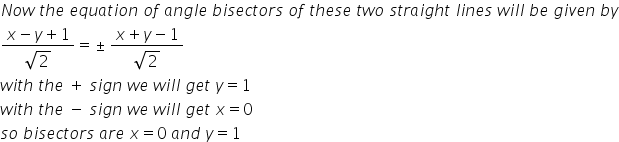
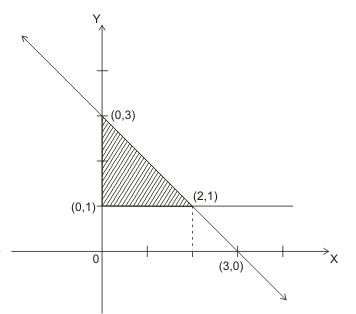
So, area between x + y = 3, x = 0 and y = 1 is given by
A = 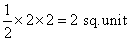
Answered by | 13 Aug, 2016, 01:48: AM
Concept Videos
CBSE 12-science - Maths
Asked by NITISH DAS | 15 Apr, 2020, 00:13: AM
CBSE 12-science - Maths
Asked by lovemaan5500 | 29 Nov, 2019, 16:18: PM
CBSE 12-science - Maths
Asked by dineshchem108 | 05 Jul, 2019, 17:58: PM
CBSE 12-science - Maths
Asked by dineshchem108 | 05 Jul, 2019, 17:56: PM
CBSE 12-science - Maths
Asked by akshitaasia | 20 Mar, 2018, 14:58: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 12 Aug, 2016, 23:02: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 12 Aug, 2016, 23:48: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM




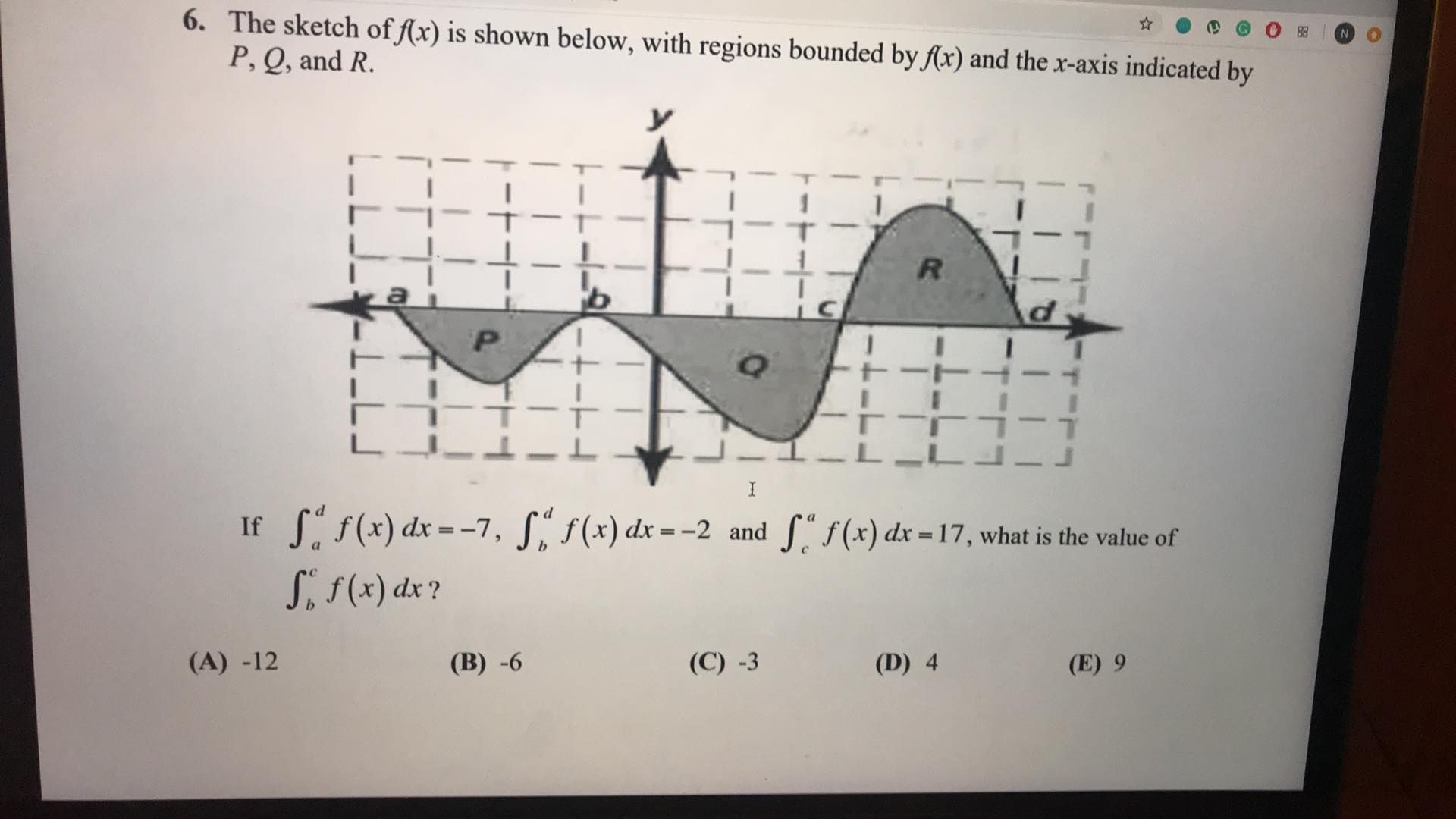
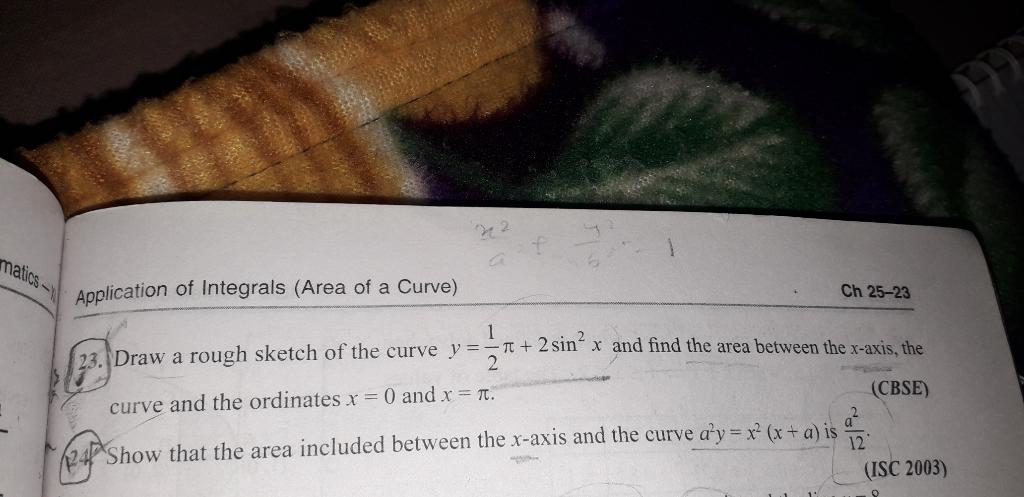

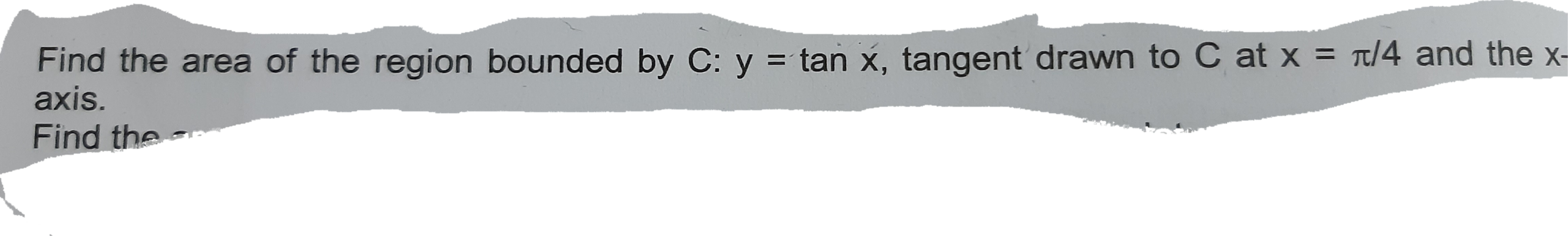

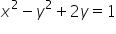 .
.