Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

Divide a line segment of length 8 cm in the ratio 3:2.
Asked by Topperlearning User | 13 Dec, 2013, 02:59: AM
answered-by-expert Expert Answer

 

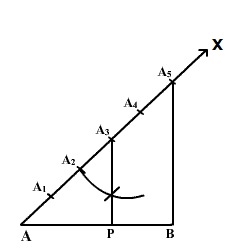
Steps of construction.

 

i. Draw a line segment AB = 8 cm.

ii. Draw any ray making an acute angle BAX with AB.

iii. Along AX mark 5 (3 +2) points A1, A2, A3, A4 and A5 such that AA1 = A1A2 = A2A3 = A3A4 = A4A5.

iv. Join BA5

v. Through A3 draw a line A3P parallel to A5B by making an angle equal to AA5B at A3 intersecting AB at point P.

The point P so obtained is the required point, which divides AB internally in the ratio 3: 2

Answered by | 13 Dec, 2013, 04:59: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
Draw a triangle ABC with sides BC= 6cm, AB= 5cm, and angle ABC =60. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Asked by sangyaswarupa | 20 May, 2021, 09:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Construct a triangle of sides 4,5,6cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle  
Asked by gaganarora2018 | 01 Dec, 2019, 09:00: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Construct a Δ ABC in which AB = 6 cm, ∠A = 30° and ∠B = 60°, Construct another ΔAB’C’ similar to ΔABC with base AB’ = 8 cm.
Asked by jaiacharya18 | 18 Feb, 2019, 01:35: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Draw a line segment AB = 6 cm. Divide it externally in the ratio 3: 5
Asked by Topperlearning User | 27 Jul, 2017, 01:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Draw a line segment AB = 6 cm. Divide it externally in the ratio 5: 3. Justify the construction.
Asked by Topperlearning User | 27 Jul, 2017, 01:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Divide a line segment of length 7 cm into three parts in the proportion 2: 3: 4.
Asked by Topperlearning User | 27 Jul, 2017, 01:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Divide a line segment of length 9 cm internally in the ratio 4: 3. Also, give the justification.
Asked by Topperlearning User | 27 Jul, 2017, 01:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Divide a line segment of length 8 cm in the ratio 3:2.
Asked by Topperlearning User | 13 Dec, 2013, 02:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Construct a right angled triangle whose hypotenuse measures 6cm and the length of one of whose sides containing the right angle is 4 cm.
Asked by Topperlearning User | 27 Jul, 2017, 01:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Construct a triangle similar to a given triangle ABC such that each of its sides is two thirds of the corresponding sides of triangle ABC. It is given that BC= 6 cm, angle B = 50oand angle C = 60o.
Asked by Topperlearning User | 27 Jul, 2017, 01:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×