CBSE Class 12-science Answered
Derivation of compound microscope
Asked by phenomenal1ajisback | 20 Feb, 2020, 20:08: PM
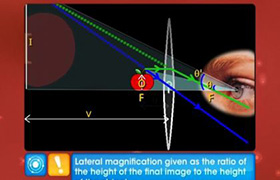
A schematic diagram of a compound microscope is shown in Figure. The lens nearest the object, called the objective,
forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece,
forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece,
which functions essentially like a simple microscope or magnifier, produces the final image, which is enlarged and virtual.
The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image
The first inverted image is thus near (at or within) the focal plane of the eyepiece, at a distance appropriate for final image
formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect
to the original object. We now obtain the magnification due to a compound microscope.
The ray diagram of figure shows that the (linear) magnification due to the objective, namely h′/h, equals
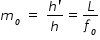 ................(1)
................(1)where we have used the result , tanβ = h/fo = h'/L
Here h′ is the size of the first image, the object size being h and fo being the focal length of the objective.
The first image is formed near the focal point of the eyepiece. The distance L, i.e., the distance between the
second focal point of the objective and the first focal point of the eyepiece (focal length fe ) is called the tube length
second focal point of the objective and the first focal point of the eyepiece (focal length fe ) is called the tube length
of the compound microscope.
As the first inverted image is near the focal point of the eyepiece, we use the simple microscope magnification equation
to obtain the (angular) magnification me .
when the final image is formed at the near point, we have, 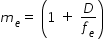
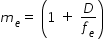
When the final image is formed at infinity, the angular magnification due to the eyepiece is
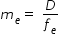
Thus, the total magnification , when the image is formed at infinity, is

Clearly, to achieve a large magnification of a small object (hence the name microscope), the objective and eyepiece
should have small focal lengths.
Answered by | 20 Feb, 2020, 21:42: PM
Concept Videos
CBSE 12-science - Physics
Asked by tannudahiya80536 | 20 Dec, 2022, 13:13: PM
CBSE 12-science - Physics
Asked by kamleshstarone392 | 16 Apr, 2022, 06:26: AM
CBSE 12-science - Physics
Asked by shijurlytepz | 12 Oct, 2021, 18:56: PM
CBSE 12-science - Physics
Asked by khanhill543 | 31 Dec, 2020, 00:20: AM
CBSE 12-science - Physics
Asked by ABHILASHA | 15 Sep, 2020, 18:23: PM
CBSE 12-science - Physics
Asked by akgujrati04 | 22 Aug, 2020, 19:06: PM
CBSE 12-science - Physics
Asked by mazhartahsildar143 | 02 May, 2020, 13:32: PM
CBSE 12-science - Physics
Asked by govtsecschoolnayaganv051 | 24 Feb, 2020, 16:17: PM
CBSE 12-science - Physics
Asked by phenomenal1ajisback | 20 Feb, 2020, 20:08: PM
CBSE 12-science - Physics
Asked by singhalakash8958 | 03 Mar, 2019, 22:11: PM