ICSE Class 10 Answered
A metal wire of resistance of 6? is stretched so that its length is increased to thrice its original length.
Calculate its new resistance.
Asked by om.chaudhari1673 | 23 Jan, 2019, 16:43: PM
When the metal wire is streched so that its length is increased thrice, its diameter will decrease.
This fact has to be taken into account while calculating the change in resistance.
when the wire is stretched its volume remain constant. If L and D are initial length and diameter respectively,
and the modified length and diameter are 3L and D' due to stretching,
then we have L×D2 = 3L×(D')2
Resistance is directly proportional to length and inversley proportional to area or square of diameter.
Let R be the initial resistance and R' be the modified resistance due to stretching
Hence 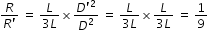
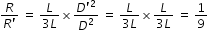
hence new resistance will be 9 times of its initial value . New resistance is 9×6 = 54Ω
Answered by Thiyagarajan K | 23 Jan, 2019, 17:41: PM
Application Videos
Concept Videos
ICSE 10 - Physics
Asked by anubhutiupadhaya | 04 Mar, 2024, 13:04: PM
ICSE 10 - Physics
Asked by navycuber2738 | 29 Feb, 2024, 14:14: PM
ICSE 10 - Physics
Asked by vijayprabath7 | 28 Jan, 2024, 16:41: PM
ICSE 10 - Physics
Asked by foodonly742 | 02 Jan, 2024, 11:06: AM
ICSE 10 - Physics
Asked by krishnathakurt139 | 06 Dec, 2023, 21:23: PM
ICSE 10 - Physics
Asked by ayanpal713143 | 27 Nov, 2023, 21:32: PM
ICSE 10 - Physics
Asked by imunilu786 | 29 Oct, 2023, 14:35: PM
ICSE 10 - Physics
Asked by praggya.srivastava.g1972 | 13 Oct, 2023, 10:51: AM
ICSE 10 - Physics
Asked by praggya.srivastava.g1972 | 11 Sep, 2023, 20:48: PM
ICSE 10 - Physics
Asked by praggya.srivastava.g1972 | 10 Sep, 2023, 22:52: PM












