CBSE Class 12-science Answered
A man is moving away from a 40 m high tower at a speed of 2m/s . find the rate at which angle of elevation of the top of the tower is changing when he is at a distance of 30m from foot of tower. Assume that eye level of the man is 1.6 m from the ground.
explain in great detail
Asked by haroonrashidgkp | 08 Sep, 2018, 04:16: PM

Answered by Sneha shidid | 10 Sep, 2018, 09:52: AM
Concept Videos
CBSE 12-science - Maths
Asked by haroonrashidgkp | 08 Sep, 2018, 04:16: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 08:00: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 08:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:18: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:20: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:22: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:29: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 09:54: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 10:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 06 Aug, 2014, 10:17: AM




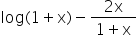 is increasing or decreasing
is increasing or decreasing