Work and Energy
Work and Energy Synopsis
Synopsis
Work & Work – Energy Theorem
- Work is any physical or mental activity that one does in performing daily tasks. However, in scientific parlance, work is done when a force produces motion in an object.
- When a boy pushes a small toy, he is able to move it. Thus, work is said to be done on the toy.
- However, few humans pushing a huge stone cannot move it in spite of putting in a lot of effort. Thus, work is not done on the stone as it does not move.
- Thus, work depends on two factors:
o Magnitude of force applied to an object.
o Distance/displacement through which the object moves. - Work done in moving a body is equal to the product of force exerted on the body and the distance moved by the body in the direction of force.
Work = Force × Distance
W = F × s - If a retarding force is applied to a body moving in a particular direction, then the work done is negative.
W = F × -s OR W = -F ×s - Thus, work can be positive, negative or zero.
- Work is a scalar quantity.
- The SI unit of work is newton metre (N m) or joule (J).
Expression of Work
- The displacement of a body need not always be in the direction of force.
- Consider the following case.
- Displacement is AC which is at an angle θ with the horizontal.
- Thus, the displacement along the direction of force is given by the horizontal component of displacement.
- Hence, work done is W = F × AB
- From right angled triangle ABC, we have
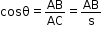
- Thus, the expression of work is
W = Fs Cosθ - Thus, we can conclude that, the amount of work done is the product of force, displacement and the cosine of angle between the force and displacement.
CASES:
- If displacement is in the direction of force, that is, θ = 0°.
Hence, the work done is, W = F × s
This work is maximum and positive. - If displacement is normal to the direction of force, that is, θ = 90°.
Hence, the work done is, W = 0.
Thus, no work is done.
Also, if displacement is zero, then the work done is zero. This is the case when a body is performing circular motion. - If displacement is in the direction opposite to that of force, that is, θ = 180°.
Hence, the work done is, W = -F × s - This work is minimum and negative.
Work Done By Gravity
- If a body of mass m moves down from a height h, the force of gravity or weight acts on the body through a displacement h.
- Thus, work done by the force of gravity is
W = Force × displacement
= Weight × height
= mg × h - Similarly, if the body is thrown up to a height h, the work done by gravity is
W = -mg × h
Work Energy Theorem
Statement
Work done on a body by a resultant force acting on it is equal to the change in the kinetic energy of the body
∴ work done, W = ∆ KE
where, ∆KE is the change in kinetic energy.
Relation between kinetic energy and momentum: -
K.E. of body is given as,
K = ½ mv2 = ½ pv = ½ (p2/2m)
Kinetic Energy and Potential Energy
Kinetic Energy
- A moving object can do work, and a fast-moving object can do more work.
- The energy possessed by an object on account of its motion is known as kinetic energy.
- Consider an object of mass m, moving with initial velocity u. Let it be displaced through a distance s when a constant force F acts on it in the direction of its displacement. The work done is
W = F × s - The work done on the object will cause a change in its velocity. Let its velocity change from u to v. Let ‘a’ be the acceleration produced.
- We know that
V2 - U2 = 2as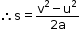
- We also know that F = ma
- Thus, the work done is
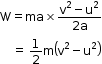
- So, we can say that work done is equal to the change in kinetic energy of the object.
- If the object starts from rest, then u = 0. Thus, we have
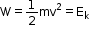
- Hence, the kinetic energy of a body is
o Directly proportional to the mass of the body.
o Directly proportional to the square of the velocity of the body.
Potential Energy
- If work is done on an object and it is not used in changing the velocity of the object, then that work is stored inside the object as potential energy.
Work is done in pulling the spring. This is stored as potential energy. - The energy possessed by an object on account of its position or configuration is known as kinetic energy.
Potential Energy of an object at a height
- To raise a body to a certain height, work is done against gravity.
- The gravitational potential energy of an object at a point above the ground is defined as the work done in raising it from the ground to that point against gravity.
- The force required to raise the object is equal to the weight F = mg of the object. If it is raised to a height h, then the work done is W = mg × h
- This work is stored in the body as potential energy.
- Work done by gravity depends on the initial and final positions and not on the path taken to raise it to the specified height.
- The potential energy is the same when the object is lifted from A to B along path 1 and path 2.
Conservative and non – conservative Forces
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken.
For e.g., Gravitational force, magnetic force etc.
A non-conservative force is the one for which work done depends on the path.
For e.g., frictional force.
Friction does more work on the block if one slides it along the indirect path across the tabletop.
The longer the path, the more work friction does.
Transformation and Conservation of Energy
- According to the law of conservation of energy, energy can neither be created nor can it be destroyed. It only changes from one form to another.
- Conservation of mechanical energy: The total mechanical energy of an isolated system at any instant is equal to the sum of its kinetic energy and the potential energy.
- According to the law of conservation of mechanical energy, whenever there is an interchange between the potential energy and the kinetic energy, the total mechanical energy remains constant, i.e., K + U remains constant when there are no frictional forces.
- Consider a body of mass m freely falling under gravity from a height h.
At position A:
Initial velocity of body = 0
Thus, kinetic energy = K =0
Potential energy = U = mgh
Hence, total energy = K + U = mgh
Initial velocity of body = 0
Thus, kinetic energy = K =0
Potential energy = U = mgh
Hence, total energy = K + U = mgh
At position B:
Let v1 be the velocity acquired by the body after falling through distance x.
Then, u = 0, S = x, a = g
From equation v2 = u2 + 2aS, we have
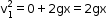
Thus, kinetic energy is
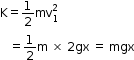
Now at B, height of body above the ground = h – x
Thus, potential energy is = mg (h - x)
Hence, total energy = K + U = mgx + mg(h - x) = mgh
At position C:
Let v be the velocity acquired by the body on reaching the ground.
Then, u = 0, S = h, a = g
From equation v2 = u2 + 2aS, we have
Let v1 be the velocity acquired by the body after falling through distance x.
Then, u = 0, S = x, a = g
From equation v2 = u2 + 2aS, we have
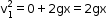
Thus, kinetic energy is
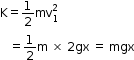
Now at B, height of body above the ground = h – x
Thus, potential energy is = mg (h - x)
Hence, total energy = K + U = mgx + mg(h - x) = mgh
At position C:
Let v be the velocity acquired by the body on reaching the ground.
Then, u = 0, S = h, a = g
From equation v2 = u2 + 2aS, we have
v2 = 0 + 2gh = 2gh
Thus, kinetic energy is
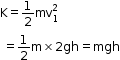
Now at C, height of body above the ground = 0
Thus, potential energy is 0.
Hence, total energy = K + U = mgh + 0 = mgh
Thus, kinetic energy is
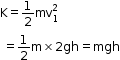
Now at C, height of body above the ground = 0
Thus, potential energy is 0.
Hence, total energy = K + U = mgh + 0 = mgh
• Thus, the mechanical energy always remains constant. Hence, mechanical energy is conserved.
Power
- Power is rate of doing work.
- Some machines do work at a faster rate, whereas some do at a slower rate. A stronger person can do a work in relatively less time.
- Power is defined as the rate of doing work or the rate of transfer of energy.

- Power is a scalar quantity.
- Power can also be written as

Here, v is the average speed of the body. - If displacement is at an angle θ, then the power is

- Its SI unit is watt (W) or joule per second (J/s) and its C.G.S. unit is erg per second (erg/s).
- Another unit of power is kilowatts (kW).
o1 kW = 1000 W
o1 MW = 106 W - Another unit of power is the horse power which is generally used in mechanical engineering. 1 horse power = 746 W = 0.746 kW.
Download complete content for FREE 

