Motion
Motion Synopsis
Synopsis
Introduction to Motion
- A particle is said to be in motion if its position, relative to the surroundings, changes with respect to time.
- A body which remains stationary (i.e., no change in position) is said to be at rest.
- Motion and rest refer to the state of bodies described in relation to its surroundings.
- The movement of a body is called motion. Rest and motion are relative terms. Thus, a body is said to be in motion when its position changes continuously with respect to a stationary object taken as a reference point.
- Suppose a body is moving very fast (e.g. train, rocket etc.), then it can be easily seen that it is in motion. Now, suppose a body is moving very slowly (e.g. snail, hour hand of watch etc.), then it is difficult to observe its motion.
Scalars and Vectors
Scalars
- In Physics, we can classify quantities such as velocity, speed, acceleration and position as scalars or vectors.
- Direction is associated with a vector but not with a scalar.
- A scalar quantity is a quantity only with magnitude. It is specified completely by a single number, along with a proper unit.
- Examples: The distance between two points, mass of an object, the temperature of a body and the time at which a certain event happened.
- Scalars can be added, subtracted, multiplied and divided just as the ordinary numbers.
Vectors
- A vector quantity is a quantity which has both magnitude and direction.
- A vector is specified by giving its magnitude by a number and its direction.
For example, displacement, velocity, acceleration and force.
Distance and Displacement
- Distance travelled is the actual length of the path covered by a moving object irrespective of the direction in which it is travelling.
- Displacement is defined as the shortest distance between the initial and final positions of the object along with the direction of its travel.
- Distance travelled has only magnitude associated with it, whereas displacement is associated with both magnitude and direction.
- Thus, distance is known as a scalar quantity and displacement is known as a vector quantity. Both the quantities are denoted by s; the only difference being that distance has magnitude and displacement has magnitude and direction.
- Distance covered by a moving object can never be zero. However, the displacement of that object can be zero.
o Example: An object starts its motion at a point. After travelling along some path, it returns to the same point. Thus, its initial and final positions are the same. Hence, its displacement is zero.
Uniform and Non-uniform Motion
- An object is said to have uniform motion if it travels equal distances in equal intervals of time, no matter how small these time intervals are.
- If we plot a distance–time graph for uniform motion, then it will be a straight line.
An object is said to have non-uniform motion if it travels unequal distances in equal intervals of time. - If we plot a distance–time graph for non-uniform motion, then it will be a curved line.
- Examples:
o Uniform motion: A motorcycle travelling with a constant speed of 5 m/s will cover equal distances of 5 m for every 1 s.
o Non-uniform motion: A body dropped from the top of a building is acted upon by gravity. Hence, its distance will increase with each interval of time. - Thus, to find out the type of motion, we should draw a distance–time graph. If it is a straight line, then it is uniform motion. If it is a curved line, then it is non-uniform motion.
- The graph of a freely falling body is a curved line. Motion of a freely falling body is accelerated. Thus, we can say that non-uniform motion is an accelerated motion.
Speed and Velocity
Speed
- Speed is a quantity which tells how fast the body is moving.
- It is defined as the distance travelled by an object per unit time.
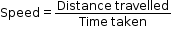
- If s is the distance travelled in time t, then the speed v is given as
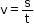
- The SI unit of speed is metre per second and is written as m s−1. The CGS unit of speed is centimetre per second and is written as cm s−1.
- Speed is a scalar quantity, as only the magnitude is needed to be specified.
Instantaneous Speed
- Instantaneous speed is the speed of a particle at a given instant. It is defined as the ratio of the distance travelled in an extremely small interval of time tending to zero.
Average Speed
- The average speed of a body is the total distance travelled by a body divided by the total time taken to cover this distance.
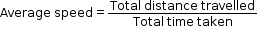
Uniform Speed
- Uniform speed is possessed by an object when it travels equal distances in equal intervals of time, no matter how small these time intervals may be.
Variable Speed
- A body has a variable speed if it does not cover equal distances in equal intervals of time.
Example: The car moving on crowded street have variable speed.
Velocity
- The velocity of a body is defined as the distance travelled by an object per unit time in a given direction.
- We know that the distance travelled in a given direction is known as displacement.
- If s is the displacement of the object in time t, then the velocity v is given as
- The SI unit of velocity is metre per second and is written as m s−1. The CGS unit of velocity is centimetre per second and is written as cm s−1.
- Velocity is a vector quantity, as both the magnitude and direction are needed to be specified.
- Thus, the velocity of an object can be changed by changing
oThe speed of the object.
oThe direction of the object, keeping its speed constant.
oBoth speed and direction of the object.
Instantaneous Velocity
- It is the velocity of the particle at a given instant. The direction of instantaneous velocity is along the tangent drawn to the curve describing the path at that instant if the body undergoes curvilinear motion.

Uniform Velocity
- Uniform velocity is possessed by an object when it travels in a specified direction in a straight line and covers equal distances in equal intervals of time, no matter how small these time intervals may be.
Average Velocity
- When the velocity of an object is changing at a uniform rate, then the average velocity is given as the arithmetic mean of the initial and final velocity in a particular time interval.

- If u is the initial velocity and v is the final velocity for a given time interval t, then the average velocity
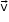 of the object is given as
of the object is given as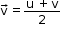
Variable Velocity
- If a body undergoes unequal displacements in equal intervals of time, then the body is said to possess variable velocity. Velocity is said to be variable if there is a change either in its magnitude or in its direction or both.
Acceleration
- Acceleration of a body is defined as the rate of change of its velocity with time.
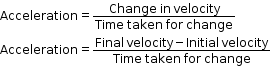
- If ‘u’ is the initial velocity, ‘v’ is the final velocity and t is the time taken, then the acceleration ’a’ of the body is given as
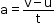
- The SI unit of acceleration is metre per second square and is written as m s−2. The CGS unit of acceleration is centimetre per second square and is written as cm s−2.
- Acceleration is a vector quantity.
- For an object moving with uniform velocity, the acceleration is zero.
Uniform Acceleration
- A body is said to possess uniform acceleration if it travels in a straight line and its velocity increases by equal amounts in equal intervals of time.
oExample 1: Motion of a freely falling object.
oExample 2: Motion of a ball rolling down an inclined plane. - The velocity–time graph of a body having uniform acceleration is a straight line.
Non-Uniform Acceleration
- A body is said to possess non-uniform acceleration if its velocity increases by unequal amounts in equal intervals of time.
oExample 1: Motion of a vehicle on a crowded city road.
oExample 2: Motion of a 110 m hurdles sprinter in a race.
Retardation
- When the velocity of a body increases with time, it is called acceleration. However, if the velocity decreases, then it is called retardation, deceleration or negative acceleration.
- Retardation is also measured as change in velocity per time taken for change.
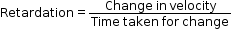
o Example: When a person opens a parachute, its velocity goes on decreasing.
Study of Motion Through Various Graphs
- If the graph of motion of an object is known, then its speed, distance travelled and acceleration can be calculated.
- Three kinds of graphs can be plotted.
Distance-Time graph (or displacement-time graph)
- The distance–time graph of a body moving at uniform speed is a straight line.
- Speed is distance travelled per unit time.
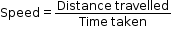
- From the graph, we have
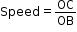
- But, the slope of the graph =
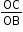
- Thus, the slope of the distance–time graph gives the speed of the object.
- If the speed of the object is non-uniform, then the graph will be a curved line.
- If a displacement–time graph is drawn, then the slope will give the velocity of the object.
Speed-Time Graph (or Velocity-Time Graph)
- There are three types of speed–time graphs for a body.
Speed–Time Graph when Speed remains Constant
- If the speed–time graph of a body is a straight line parallel to time axis, then the speed is constant or uniform.
- Speed is the distance travelled per unit time.
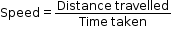
- Thus, we have Distance travelled = Speed × Time taken.
- Now, to find the distance travelled at point C, we draw a perpendicular CB.
- Thus, speed and time at C is
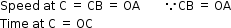
- Thus, the distance travelled is
Distance travelled = OA × OC = Area of rectangle OABC - Thus, in a speed–time graph, the area enclosed by the speed–time curve and the time axis gives the distance travelled by the body.
- Also, we can conclude that the velocity–time graph of an object moving with constant velocity is a straight line parallel to the time axis.
- The area enclosed by the velocity−time curve and the time axis gives the displacement of the body.
Speed–Time Graph when the Speed Changes at a Uniform Rate
- The speed–time graph of a body with uniform changing speed will be a straight line.
- Acceleration is change in speed per time taken for the change.
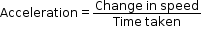
- From the graph, we get the change in speed and time as

- But the slope of the graph =

- Thus, the slope of the speed–time graph gives the acceleration of the object.
- Also, distance can be calculated from the speed–time graph as
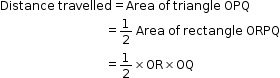
- The speed–time graph of an object showing upward slope gives uniform acceleration, and similarly, the speed–time graph of an object showing downward slope shows uniform retardation.
Speed–time graph when the initial speed of the body is not zero
- The speed–time graph for an object moving with uniformly changing speed and initial speed not equal to zero is shown.
- The acceleration in this case is
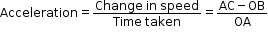
- Distance can be calculated from the graph as

Speed–Time Graph when the Speed Changes at a Non-Uniform Rate
- When an object is moving with non-uniform changing speed, then the speed–time graph is a curved line showing non-uniform acceleration.
Acceleration-Time Graph
- In this graph, acceleration is plotted along Y-axis and time along X-axis.
- When body is moving with uniform acceleration, a is constant.
- Body moving with constant velocity, a = 0
- Uses of Acceleration–time Graph:
1. Acceleration at any intermediate time can be determined.
2. Area under the curve gives the change in magnitude of velocity i.e. (v − u).
Equations of Motion
- The three equations of motion can be derived with the help of velocity (speed) – time graph as follows:
- Consider the velocity–time graph of a body with initial velocity u at point A.
- It has an uniform acceleration from A to B as its velocity changes uniformly in time t. After the time t, its final velocity is v.
- In the graph, u = OA, v = CB, t = OC.
- We draw perpendicular CB from point C and draw AD parallel to OC. Also, BE is the perpendicular from B to OE.
First Equation: v = u + at
- Initial velocity of the body is u = OA and final velocity is v = CB.
- From the graph, we have CB = CD + DB
- Therefore, v = CD + DB
- Now, from the graph, we have DC = OA.
- Therefore, v = DB + OA.
- Since u = OA, we have
v = DB + u…… (1) - Now, we know that the slope of the velocity–time graph gives the acceleration a.
- Thus, we have
a = Slope of line AB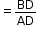
- But from the graph, AD = OC = t. Thus, acceleration is written as
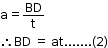
- Thus, substituting equation (2) in (1), we get v = u + at.
- This is how the first equation of motion is derived from the graphical method.
Second equation: s = ut + ½ at2
- Suppose a body travels a distance s in time t. The distance travelled is given as the area between the graph AB and the time axis OC, i.e. the distance travelled is equal to the area of the figure OABC.
Distance travelled = Area of OABC
= Area (rectangle OADC) + Area(Triangle ABD) - Now, the area of the rectangle is given as
Area(rectangle OADC) = OA × OC
= u × t = ut - The area of the triangle is given as
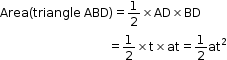
- Thus, the distance travelled is
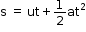 .
.
Third equation: v2 = u2 + 2as
- The distance travelled is equal to the area of the figure OABC. Because OABC is a trapezium,
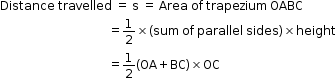
- Now, we have OA + BC = u + v and OC = t . Thus, the distance travelled is
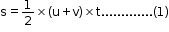
- Eliminate t from the above equation with the help of the first equation of motion as
v = u + at
at = v - u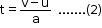
- Substitute equation (2) in equation (1).
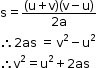
- Thus, the third equation is v2 = u2 + 2as.
Equations of motion under the influence of gravity
- The equation of acceleration due to gravity is
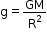 . From this equation, we can conclude that g is independent of the mass of the object that is falling. Thus, any object big or small, solid or hollow, should fall with the same acceleration.
. From this equation, we can conclude that g is independent of the mass of the object that is falling. Thus, any object big or small, solid or hollow, should fall with the same acceleration. - The equations of motion become valid for a falling object as g is constant near the Earth. These equations in terms of g are
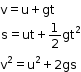
- Here, g should be positive if it is in the direction of motion, and it should be negative if it moving against the acceleration due to gravity.
- Equations of motion of body dropped from a certain height: -
u = 0,
s = h (height from which the object is dropped)
a = +g
Thus,
1. v = gt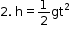
3. v2 = 2gh
Thus, time of descent is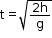
- Equations of motion of body when it is projected upward: -
s = h (height from which the object is dropped)
a = – g
Thus,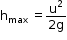
For body projected vertically upward, the time of ascent (ta) is time taken to reach the maximum height.
ta =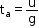
A vertically projected body after reaching its maximum height (hmax) starts falling and behaves as a body dropped from maximum height. The time that it takes to reach the ground from the maximum height, can be given by,
Thus,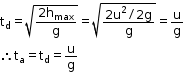
Thus, time of ascent is equal to time of descent when body is projected vertically up.
Time of flight (tf)
The total time during which a body moving under gravity remains in air above the plane of projection.
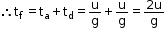
Uniform Circular Motion (U.C.M.)
- When an object moves in a circle, its motion is called circular motion.
- Examples
oMotion of a giant wheel in a funfair.
oMotion of the wheel of a bicycle. - When an object moves along a circular path, its direction of motion as well as speed changes continuously.
- Thus, the motion is said to be an accelerated motion as the speed (or velocity) keeps changing.
- Now, when the body moves in a circle with uniform speed, its motion is known as uniform circular motion.
- This may suggest that the motion is not accelerated. However, the direction of speed changes at each and every point along the circle. Thus, even though the speed is constant, its direction changes. Hence, the velocity changes and is an accelerated motion.
- The force needed to make an object travel in a circular path is known as centripetal force.
Examples of Uniform Circular Motion
- Moon revolving around the earth: The moon revolves around the earth in a circular orbit. It completes one revolution of its orbit in a period of about 29.3 days.
- The tip of the seconds’ hand of a clock: The tip of the seconds’ hand of a clock shows uniform circular motion. It completes every circle in a period of 60 seconds.
Speed of an Object in Uniform Circular Motion
- When an object completes one round around the circle, it traverses a distance equal to the circumference of the circle.
- Let an object move in a circle of radius r. Thus, the circumference is equal to 2πr.
- Now, the speed of the object is given as
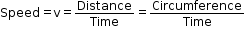
- Thus, the speed of the object performing uniform circular motion is
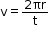 .
.
Download complete content for FREE 

