Hydrostatistics

Synopsis

Pascal’s Law

• Pascal’s law explains how pressure is transmitted in liquids.
• It states that, “The pressure exerted anywhere in a confined liquid is transmitted equally and undiminished in all the directions throughout the liquid”.
• Pascal’s law can be demonstrated with the help of the following experiment:
  o Take a glass flask with narrow tubes coming out from its sides and bottom. The flask is provided with an air-tight piston at its mouth. 
  
  
  
  o Fill the flask with water. The water in each tube will be at the same level. 
  o The initial level of water in each tube is shown by the dotted red line. 
  o Now, push the piston down into the flask gently. It is observed that jets of water rise out from each tube, reaching the same height which is shown by the dotted blue line. 

Application of Pascal’s Law

• Hydraulic press, hydraulic jack and hydraulic brakes work on Pascal’s law of transmission of pressure.
• The principle of the working of these hydraulic machines is, “A small force applied on a smaller piston is transmitted to produce a large force on the bigger piston”.
• Consider two cylindrical vessels P and Q connected by a horizontal tube R. The vessels contain a liquid, and they are provided with water-tight pistons A and B.
  
  
  
  
  
• The vessel P is of smaller diameter than the vessel Q. Let the area of cross section of the vessel P be A₁ and that of the vessel Q be A₂. A weight is placed on the piston A. It exerts a force F₁ on the piston A. Therefore, the pressure applied on the piston A is
  
  
• According to Pascal’s law, the pressure exerted on piston A is transmitted through the liquid to piston B. Therefore, the upward pressure on B is
  
  
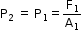
• Hence, the force on piston B is
  F₂ = Pressure on piston B is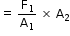
  
  
  
  Therefore, we have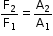
  
  
  
• Since, A₂ > A₁, we get F₂ > F₁.

Buoyancy

• Whenever an object is immersed in water or any other liquid, it appears to lose some weight and feels lighter.
• The weight of the object exerts a force on the liquid. The liquid also exerts a certain amount of force on the object in the upwards direction. This force is called buoyant force.
• The tendency of a liquid to exert an upward force on any object immersed in it is called buoyancy.
• The upward force exerted by a liquid is also called upthrust.

Why Objects Float or Sink when Placed on a Surface of Water

• If the downward gravitational force of an object is greater than the upward buoyant force of water, then the object sinks. However, if the gravitational force is less, then the object floats.
  
  
  
  The light plastic ball floats, while the heavy marble sinks.
  
  
• Objects with a density lesser than water float on water, and objects with a density greater than water sink in it.
• The magnitude of buoyant force acting on an object immersed in a liquid depends on:
  o Volume of object immersed in the liquid. This is because the density changes with volume.
  o Density of the liquid.

 

Archimede’s Principle

• When an object is immersed wholly or partially in a fluid, it experiences an upward force that is equal to the weight of the fluid displaced by it.
  Buoyant force acting on an object = weitght of fluid displaced by that object
• Gases however exert a very negligible buoyant force on the objects placed in them.
  
  
  
  
• A boat floats on water due to the Archimedes’ principle. The boat displaces water equal to its own weight. This displaced water exerts buoyant force to balance the weight of the boat and keep it floating on water.

 

Applications of the Archimedes’ Principle

• The Archimedes’ principle is used in determining the relative density of a substance.
• Hydrometers used to determine the density of liquids are based on the Archimedes’ principle.
  
  
  
  
• Lactometers used to determine the purity of milk are based on the Archimedes’ principle.
• The Archimedes’ principle is also used in designing ships and submarines.

 

Density

• The density of a substance is defined as mass per unit volume.
• Different substances have different densities.
• It is a scalar quantity and is represented by the Greek letter ρ.
  
  
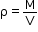
•  Its SI unit is kg m−3 and its CGS unit is g cm⁻³.Most substances expand on heating and contract on cooling.
• Thus, the density of a substance increases with decrease in temperature and decreases with increase in temperature.

 

Relative Density (RD)

• It is convenient to express the density of a substance in comparison to the density of water.
• The relative density of a substance is the ratio of its density to that of water at 4°C.
  
  
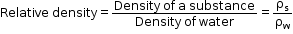
• It is also given as the ratio of the mass of the substance to the mass of equal volume of water at 4°C.
  
  
  
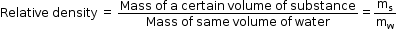
• Because it is a ratio of similar quantities, it has no units.
• In the SI system, the density of water is 1000 kg m⁻³. Thus, we have
  
  
  
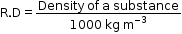
  ∴ Density in kg m^-3 = 1000 R.D
• Now, the density of water in the CGS system is 1 g cm⁻³. Thus, we have
  
  
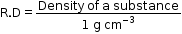
  ∴ Density in g cm^-3 = R.D

 

Distinction between Density and Relative Density

 

 

 

 Relative Density of a Solid by Archimedes’ Principle

• From the definition of relative density, we have
  
  
  
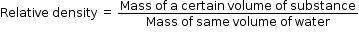
• According to Archimedes’ principle, the mass of water of volume equal to that of the body is found by finding the mass of the water displaced by the body when it is completely immersed in water. Thus, we have
  
  
  
  
• If W₁ is the weight of a body in air and W₂ is the weight of a body in water, then
  
  

 

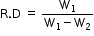
Principle of Floatation

• A body immersed in a liquid experiences two forces:
  
  o Its weight in the downward direction through its centre of gravity G.
  o The upthrust due to the liquid in the upward direction through the centre of gravity of the displaced liquid. This centre is called the centre of buoyancy B.
• The following three cases will explain when a body will sink or float.
  o Case I: When W > F_B, i.e. the weight of the body is greater than the weight of the displaced liquid.
  
  
  o The body will sink. The apparent weight of the body will be W − F_B. 
  o This case arises when the density of the solid is more than the density of the liquid.
  
  
• Case II: When W = F_B, i.e. the weight of the body is equal to the weight of the displaced liquid.
• 
  
  o The body will float with its body submerged just below the surface of the liquid. The apparent weight of the body will be zero.
  o This case arises when the density of the solid is equal to the density of the liquid.
  
  
• Case III: When W < F_B, i.e. the weight of the body is less than the weight of the liquid displaced.
  
  
  
  
• The body will float partially above the surface of the liquid. The part of the body which immerses will have a weight equal to the weight of the water displaced. 
• Also, in this case, the centre of buoyancy will be slightly lower than the centre of gravity.
• From the above three cases, we define the principle of floatation as, “The weight of a floating body is equal to the weight of the liquid displaced by its submerged part”.

 

Relation between Volume of the Submerged Part of a Floating Body, the Densities of Liquid and the Body

• We have a body of volume V and density ρ_s. 
• Let us say that the body is floating with v of its volume immersed in a liquid. Thus, the body will displace v volume of liquid. The liquid has density ρ_L.
• Thus, we have
  Weight of body W = Volume × density of body × g
  = Vρ_sg
• Now, upthrust, i.e. the weight of the liquid displaced is
  F_B = Volume of displaced liquid × density of displaced liquid × g
      = vρ_Lg
• For floatation, we have
  W = F_B
  Vρ_sg = vρ_Lg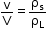
  
  
  

 

Pressure in Fluids and Atmospheric Pressure

• A substance which flows is called a fluid.
• All liquids and gases are fluids. A solid exerts pressure on a surface due to its weight. Similarly, fluids have weight, and they exert pressure on the base and the walls of the container in which they are enclosed.
• Pressure exerted in any confined mass of fluid is transmitted uniformly in all the directions.

 

Pressure exerted by a Liquid Column 

• Consider a liquid of density ρ in a vessel. We also consider a liquid column PQRS in the liquid.
  
  
  
  
• The total thrust acting on the surface PQ at a depth ‘h’ will be equal to the weight of the liquid column PQRS.
  Thrust = Weight of liquid column PQRS
            = mass × g
            = Volume × density × g
            = (Area of base PQ)(height) × density × g
            = Ahρg
• Thus, the pressure on the surface PQ is
  P =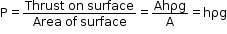  
• Now, the total pressure inside a liquid column at a depth is the sum of the atmospheric pressure on the liquid surface and the pressure due to the liquid column.
  Total Pressure = P₀ + hρg
• Hence, we can say that the pressure at a point inside the liquid depends directly on
  o The depth of the point below the surface of liquid.
  o The density of the liquid.
  o The acceleration due to gravity.
• Acceleration due to gravity ‘g’ remains constant at a particular place on Earth. Thus, pressure varies with depth and density.
• Also, because sea water is denser than river water, the pressure at a particular depth is more in sea water than in river water at the same depth.

 

Laws of Liquid Pressure

• Pressure is same in all the directions about a point in the liquid.
• In a stationary liquid, pressure is the same at all points on a horizontal plane.
• Pressure at a point inside the liquid increases with the depth from the free surface.
• Pressure at the same depth is different in different liquids. It increases with increase in density.
• A liquid seeks its own level.

 

Atmospheric Pressure

• The envelope of air surrounding the Earth is called the atmosphere.
• The thrust exerted per unit area of the Earth surface due to the column of air is called the atmospheric pressure on the Earth’s surface.
• Its value is about 1 kgf/cm² = 10⁵ Nm^-2 = 10⁵ Pa.
• We do not feel this large amount of thrust as our blood pressure balances this thrust.
• It is expressed in terms of height of mercury column. At normal temperature and pressure, the barometric height is 0.76 m of Hg at sea level. This is taken as one atmosphere.
• 1 atm = 0.76 m of Hg = 76 cm of Hg = 760 mm of Hg = 1.013 × 10⁵ Pa

 

Measurement of Atmospheric Pressure

• Atmospheric pressure is measured with the help of a barometer.
• Three types of barometers are used:
  oSimple barometer
  oFortin’s barometer
  oAneroid barometer

 

Variation of Atmospheric Pressure with Altitude

• The atmosphere can be imagined as consisting of several parallel air layers.
• Each layer experiences a pressure on it due to the thrust of the air column above it. 
• The pressure of air decreases with an increase in altitude. 
• The decrease in atmospheric pressure is due to
  oDecrease in height of the air column which causes a linear decrease in the atmospheric pressure.
  oDecrease in density of air which makes the decrease in atmospheric pressure less rapid with an increase in altitude.
• The following graph shows the variation of atmospheric pressure with height above sea level.
  
  

 

Consequences of Travelling to High Altitudes

• The air pressure reduces and hence breathing problems occur. Also, the nose may bleed because the blood pressure becomes more than the atmospheric pressure.
• A fountain pen contains some air along with the ink. The pressure of this air is air pressure at the surface of the Earth. Thus, the fountain pen will start leaking due to the difference in air pressure at high altitude compared to that at the surface.