Gravitation
Gravitation Synopsis
Synopsis
Universal Law of Gravitation
- When any object is dropped from a height, it falls towards the Earth. This is because the Earth exerts a force of attraction on that object.
- The planets revolve around the Sun. Satellites go around the planets. There is a force that acts between these bodies.
- In all these cases, the force acting is the same as explained by Newton. This force is called the gravitational force.
- According to Newton, every object in the universe attracts every other object with a force known as the gravitational force.
- If the masses of two bodies are small, then the gravitational force between them is very small. Example: A person is pulled towards the Earth. According to Newton’s third law, the person also exerts an equal and opposite force on the Earth. From Newton’s second law, the acceleration produced is inversely proportional to the mass. So, we do not see the Earth moving towards the person.
- Gravitational force is always an attractive force.
- Universal law of gravitation was given by Newton. According to this law, “Every object in the universe attracts every other object with a force which is proportional to the product of their masses and inversely proportional to the square of the distance between them”.
- Consider two objects A and B of mass M and m separated by a distance r.
- According to Newton’s law of gravitation, the force F of attraction between the two objects is given as
F ∝ Mm
Thus, combining the above two equations, we get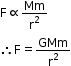
G is the proportionality constant and is known as the universal gravitation constant. - The universal gravitation constant G is independent of
o Medium between the two bodies.
o Masses of the two bodies.
o Distance of separation between the two bodies. - From the equation of force, we have
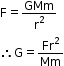
- Thus, the SI unit of G is Nm2/kg2.
- The value of = 6.67 × 10-11 N m2/kg2.
Importance of the Universal Law of Gravitation
- The universal law of gravitation successfully explained several phenomena which were believed to be unconnected:
o Force that binds us to the Earth.
o Motion of the Moon around the Earth.
o Motion of the planets around the Sun.
o Tides due to the Moon and the Sun.
Free Fall
- Whenever objects fall towards the Earth under the influence of gravitational force alone, we say that the objects are in free fall.
- The motion of an object under free fall is an accelerated one, as the magnitude of velocity keeps on changing. This acceleration is due to the gravitational force, and hence, is known as acceleration due to gravity g.
- According to Newton’s second law of motion, the force on a falling object of mass m is F = mg.
- Also, according to Newton’s law of gravitation, the force between the object and the Earth is
 .
. - Thus, we have
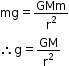
- Here, M is the mass of the Earth and r is the distance of the object from the centre of the Earth. Because the object is near the surface of the Earth, we can take r = R, the radius of the Earth.
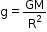
- The Earth is not a perfect sphere. As the radius of the Earth increases from the poles to the equator, the value of g becomes greater at the poles than at the equator. On an average, we can take g to be constant on or near the surface of the Earth. However, for objects far from the Earth, g goes on decreasing.
Value of g
- Substitute the values of G, M and R in equation the
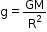 .
. - We know that G = 6.67 × 10-11 N m2/kg2, M = 6 × 1024 kg and R = 6.4 × 106m. Therefore, we get
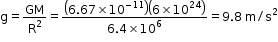
Centre of Mass and Centre of Gravity
- From the universal law of gravitation, we understand that the force of gravitation acts along the line joining the two particles. An extended body is a collection of a number of such particles.
- To identify the line of action of the gravitational force in such cases, we define a point called centre of mass.
- Centre of mass is a point within or outside a body where its whole mass can be assumed to be concentrated.
- For example, for spherical bodies like the Earth, the centre of mass is at the centre of sphere.
- For extended bodies, we say that the force of gravitation acts along the line joining their centres of mass.
- Hence, considering the Earth as a sphere, the force of gravity acts towards the centre of the Earth.
- The distance between the Earth and a body is equal to the distance between the centre of earth and the centre of mass of that body.
- The center of gravity is a geometric property of any object. The center of gravity is the average location of the weight of an object. It is the point about which the total weight of the body acts.
- We can completely describe the motion of any object through space in terms of the translation of the center of gravity of the object from one place to another, and the rotation of the object about its center of gravity if it is free to rotate.
Mass
- The quantity of matter contained in a body is called mass.
- Mass is constant and has the same value at different places and positions.
- The SI unit of mass is kilogram (kg) and the CGS unit is gram (g).
Weight
- The force with which Earth attracts a body towards its centre is called the weight of the body.
- Weight of a body is not constant.
- As weight is a force, its SI unit is newton (N).
- For a body of mass m, the weight is given as W = mg
Difference between Mass and Weight
Kepler's Laws of Planetary Motion
- The 16th century astronomer Johannes Kepler established three laws which govern the motion of planets (around the Sun) known as Kepler's law of planetary motion.
- This law also describes the law of satellites (e.g., the Moon) around the planets (e.g., the Earth).
- Kepler's laws of planetary motion are empirical in nature.
Kepler's First Law (Law of Orbits)
- All planets revolve around the Sun in elliptical orbits with the Sun situated at one of the foci of the elliptical orbit.
- This law is based on the inverse square law.
- In the above figure, the closest point P is called perihelion and the farthest point A is called aphelion. The mid-point O of the line PA is the centre of the ellipse.
- Length PO = AO is called the semi-major axis of the ellipse.
- For a circle, the two foci of the ellipse merge into one and the semi-major axis becomes the radius of the circle.
Kepler's Second Law (Law of Areas)
- The line which joins a planet to the Sun sweeps out equal areas in equal intervals of time, i.e. the areal velocity of the planet around the Sun is constant.
- The linear speed of the planet is more when closer to the Sun than when it is away from the Sun.
Area P1 S P2 ≡ Area P3 S P4
Since SP1 > SP3; therefore, P1P2 < P3P4
or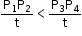
- Kepler's second law is based on law of conservation of angular momentum
mvP rP = mvA rA
or
Kepler's Third Law (Law of Periods)
- The square of the time period of revolution of a planet around the Sun is directly proportional to the cube of the semi-major axis of its elliptical orbit.
T2 µ R3
Here T = time taken by the planet to revolve around the Sun
and R = semi-major axis of the elliptical orbit
If the period of revolution of two planets are T1 and T2, and the average radii of their orbits are R1 and R2, respectively, then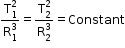
This law is also referred to as the law of periods.
Download complete content for FREE 

