Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

What is the centre of mass of sector of the circle. Explain with diagram
Asked by rushabh1234 | 17 Oct, 2019, 06:05: AM
answered-by-expert Expert Answer
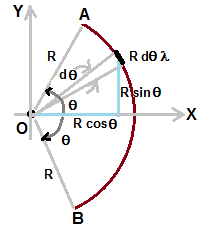
First let us find the centre of mass of thin rod bent in the form of circular arc that subtends angle 2θ at centre.
 
Let us cinsider a small element of length dl that subtends angle dθ at centre.
Let mass is distributed uniformly and λ is mass per unit length of rod .
 
mass moment of this small element along x-axis :-  ( R dθ λ ) ( R cosθ) = R2 λ cosθ dθ
 
mass moment of this small element along y-axis :-  ( R dθ λ ) ( R sinθ) = R2 λ sinθ dθ
 
x-coordinate of centre of mass of ring :- 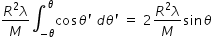begin mathsize 14px style fraction numerator R squared lambda over denominator M end fraction integral subscript negative theta end subscript superscript theta cos theta apostrophe space d theta apostrophe space equals space 2 fraction numerator R squared lambda over denominator M end fraction sin theta end style 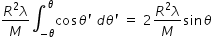........................... (1)
y-coordinate of centre of mass of ring :- 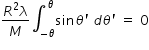begin mathsize 14px style fraction numerator R squared lambda over denominator M end fraction integral subscript negative theta end subscript superscript theta sin theta apostrophe space d theta apostrophe space equals space 0 end style 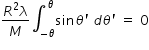  ..............................(2)
Where M is mass of whole rod.
 
Mass density λ is defined as, λ =  mass / length = M/( R 2θ )  ..................(3)
 
using the expression for λ in (3), we get x-coordinate and y-coordinate of centre of mass from eqn.(1) and (2) as
 
Centre of mass :-  [ ( R sinθ / θ ) , 0 ] .................................(4)
 
Coordinates are given in above equation, as shown in figure, considering centre of curvature of arc coincides with origin and
line connecting the origin and centre of circular arc coincides with x-axis.
-------------------------------------------------------------------
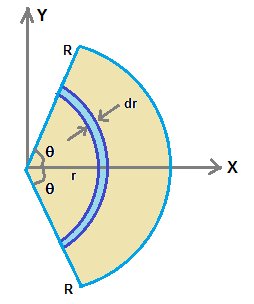
We consider sector of circular disc , angle 2θ at centre , is made up sevaral rings in the shpae of circular arc as shown in figure.
 
Since we calculated coordinates of centre of mass of circular arc, using that formula  for a circular arc ring of thickness dr,
we find the x-coordinate of centre of mass of sector of circular disc as follows
 
mass of circular arc ring = r×2θ×dr×ρ
 
where ρ is density per unit area
 
If M is total mass of sector of circular disc, then x-coordinate of centre of mass of sector of circular disc is given as
 
begin mathsize 14px style 1 over M integral subscript 0 superscript R r space cross times 2 theta cross times d r cross times rho cross times r cross times fraction numerator sin theta over denominator theta end fraction space equals space fraction numerator 2 space sin theta space rho over denominator M end fraction integral subscript 0 superscript R r squared d r space equals space 2 over 3 fraction numerator rho space R cubed over denominator M end fraction sin theta end style...............(5)
density ρ is defined as, ρ = M/ [ (2θ/2π) πR2 ] = M / [ θ R2 ] ...............(6)
 
By substituting ρ in eqn.(5),  x-coordinate of centre of mass of sector of circular disc is given as   (2/3)R (sinθ/θ)
 
x and y coordinate of centre of mass of sector of circular disc is given as  [ (2/3)R (sinθ/θ) , 0 ]
 
Coordinates are given in above equation, as shown in figure, considering centre of curvature of sector of circle coincides with origin and
midline dividing the sector of circle coincides with x-axis.
 
Answered by Thiyagarajan K | 17 Oct, 2019, 10:23: PM

Application Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
find current
question image
Asked by arivaryakashyap | 23 Apr, 2024, 10:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Three equal charges, 2⋅0 × 10 − 6 C each, are held fixed at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the rest two.
question image
Asked by ratnadeep.dmr003 | 21 Apr, 2024, 11:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Time period for a simple harmonic motion (d ^ 2 * x)/(d * t ^ 2) =- mu xis:
Asked by ksahu8511 | 19 Apr, 2024, 11:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
find the acceleration
question image
Asked by mohammedimroz | 13 Apr, 2024, 09:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
solution of 12th question
question image
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
if Bi with a mass number 211 and atomic number 83 undergoes beta decay the resultant daughter nuclei will be
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
four charges are arranged at corners of square abcd as in figur the force on charge kept at centre o is
question image
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two small conducting spheres each of mass 9×10‐⁴kg qre suspended from the same point by non conducting strings of length 100cm. they are given equal and similar charges until the strings are rqually inclined at 45° each to the vertcal. The charge on each sphere is
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
how to draw straight line graph and how to identify y-intercept and slope
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Help me
question image
Asked by nandichandi33 | 24 Mar, 2024, 09:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×