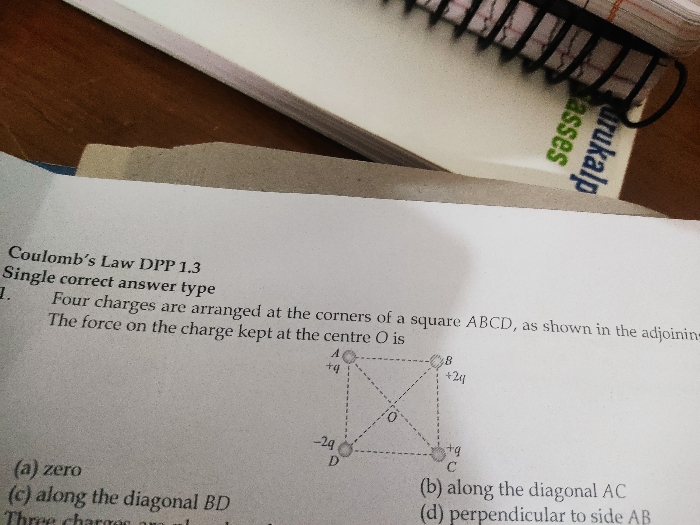JEE Class main Answered

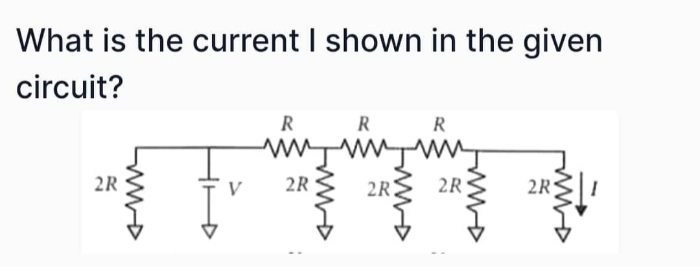
Urgent... Plz plz solve this numerical attached below.

Asked by subhrajayanta64 | 25 Aug, 2019, 03:28: AM

Expert Answer

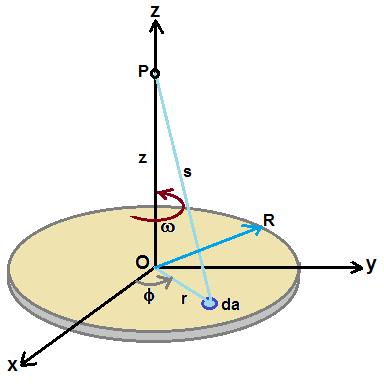
Figure shows a uniformly charged disc of radius R with uniform charge density σ per unit area.

Let the axis of disc coincide with z-axis of cartesian coordinate system and centre of disc is at origin.

If the disc is roatating with angular velocity ω, then we get current flow in circular direction due to

rotational motion of charges in the disc. This creates magnetic field in surrounding region

Magnetic vector potential A at a point P on the axis which is at a distance z due to small area element da is given by

begin mathsize 14px style bold italic A space equals space fraction numerator mu subscript o over denominator 4 pi end fraction double integral K over s bold italic d bold italic a end style

...............................(1)

where K is current density vector, K = σ ω r and area element da = dr rdφ = r dr dφ

By using these substitutions, eqn.(1) is written as

begin mathsize 14px style A space equals space fraction numerator mu subscript o over denominator 4 pi end fraction integral subscript 0 superscript R fraction numerator sigma space omega space r squared d r over denominator square root of r squared plus z squared end root end fraction space integral subscript 0 superscript 2 pi end superscript d phi space space equals space fraction numerator mu subscript o space sigma space omega over denominator 2 end fraction space integral subscript 0 superscript R fraction numerator space r squared d r over denominator square root of r squared plus z squared end root end fraction space end style

......................(2)

begin mathsize 14px style L e t space space I space equals space integral subscript 0 superscript R fraction numerator r squared space d r over denominator square root of r squared plus z squared end root end fraction space space equals space integral subscript 0 superscript R space square root of r squared plus z squared end root space d r space space space minus space z squared space space integral subscript 0 superscript R fraction numerator d r over denominator square root of r squared plus z squared end root end fraction A b o v e space i n t e g r a t i o n s space i n space R H S space a r e space w o r k e d space o u t space f r o m space t a b l e space o f space i n t e g r a l s w e space g e t comma space space I space equals space R over 2 square root of R squared plus z squared end root space minus space z squared over 2 space ln open parentheses fraction numerator R plus square root of R squared plus z squared end root over denominator z end fraction close parentheses end style

By substituting the above integration results in eqn.(2), we get Vector potential A as

begin mathsize 14px style A space equals space fraction numerator mu subscript o sigma omega over denominator 4 end fraction open curly brackets space R space square root of R squared plus z squared end root space minus space z squared space ln open parentheses fraction numerator R plus square root of R squared plus z squared end root over denominator z end fraction close parentheses close curly brackets end style

Direction of vector potential is along +ve z-axis , as per eqn.(1) [ da is vector area , direction of da is along z-axis ]

Answered by Thiyagarajan K | 25 Aug, 2019, 04:25: PM

Application Videos