CBSE Class 9 Answered
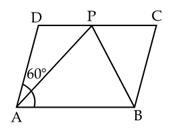
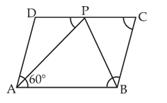
(i) ABCD
is a parallelogram in which ![]() A = 60°.
A = 60°.
AP and PB are the bisector of ![]() A and
A and ![]() B respectively.
B respectively.
![]() PAB =
PAB = ![]() PAD = 30° (AP bisects
PAD = 30° (AP bisects ![]() A)
A)
AB || CD and AP is the transversal.
![]()
![]() PAB =
PAB = ![]() APD = 30° (Alternate
angles)
APD = 30° (Alternate
angles)
In ![]() APD,
APD,
![]() PAD =
PAD = ![]() APD = 30°
APD = 30°
![]() PD = AD ...(1) (Equal sides have equal
angles opposite to them in a trangle)
PD = AD ...(1) (Equal sides have equal
angles opposite to them in a trangle)
(ii) AD || BC and AB is the transversal.
![]()
![]() A +
A + ![]() B = 180° (Sum of
adjacent interior angles is 180°)
B = 180° (Sum of
adjacent interior angles is 180°)
![]() 60° +
60° + ![]() B = 180°
B = 180°
![]()
![]() B = 120°
B = 120°
![]()
![]() PBA =
PBA = ![]() PBC = 60° (PB is
bisector
PBC = 60° (PB is
bisector ![]() B)
B)
![]() PBA =
PBA = ![]() BPC = 60° (Alternate
angles)
BPC = 60° (Alternate
angles)
In ![]() PBC,
PBC,
![]() BPC =
BPC = ![]() PBC = 60°
PBC = 60°
![]() BC = PC ...(2) (Equal sides have equal
angles opposite to them)
BC = PC ...(2) (Equal sides have equal
angles opposite to them)
(iii) CD = DP + PC
![]() CD = AD + BC [Using (1) and (2)]
CD = AD + BC [Using (1) and (2)]
![]() CD = AD + AD [AD = BC (Opposite sides of
parallelogram are equal)]
CD = AD + AD [AD = BC (Opposite sides of
parallelogram are equal)]
![]() CD = 2AD
CD = 2AD