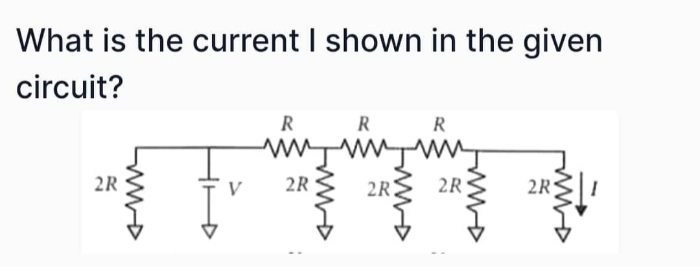
JEE Class main Answered
A point object is located at a distance of 100 cm from a screen a lens of focal and 23 CM mounted on a movable frictionless stand is kept between the source and the screen The Stand is attached to a spring of natural length 50 cm and Spring Constant800Newton per metre as shown in figure mass of the stand with lens is to kilogram how much impulse should be imparted to the stand so that a real image of the object is formed at the screen after the fixed time gap also find this time gap
Asked by hk4979169 | 14 Feb, 2021, 12:37: PM
Expert Answer
In the given image forming system, object and image capturing screen are 100 cm apart.
Let u is distance between lens and object. Let v is distance between screen (image) and lens .
It is given that u+v = 100 cm ............... (1)
we have lens equation , (1/v) + (1/u) = (1/f)...............(2)
where f = 23 cm is focal length of lens
using eqn.(1) , we rewrite eqn.(2) as , (1/v) + [ 1 / ( 100 - v ) ] = 1/23
above expression is simplified as , v2 - 100v +2300 = 0
we get v = 35.9 cm as acceptable solution to above quadratic equation .
Hence to get lens-to-image distance as 35.9 cm , spring has to be compressed to a distance ( 50 -35.9) = 14.1 cm
Force F required to compress the spring to a distance 14.1 cm as , F = kx = 800 × 0.141 ≈ 113 N
Acceleration experienced by the stand = force /mass = 113/2 = 56.5 m/s2
Time t to move a distance 14.1 cm is determined from the following equation
S = (1/2) a t2 or t = [ ( 2 S ) / a ]1/2 = [ ( 2 × 0.141 ) / 56.5 ]1/2 ≈ 0.071 s = 71 ms
Impulse = force × time = 113 × 0.071 = 7.983 N s
Time gap = 71 ms = 0.071 s
Answered by Thiyagarajan K | 14 Feb, 2021, 02:46: PM
Application Videos
-
Elastic potential energy_Restoring force and spring con ...
In this video, the restoring force and spring constant is explained. The vi... -
Expression of Elastic potential energy_2
This video describes the potential energy of spring when it is compressed o... -
Potential Energy Curve
This video describes the potential energy curve and ature of forces based o... -
Work done by static friction
This video describes effect of static friction on the work done by the obje... -
Work done in conservative field - 1
The concept of conservative field, types of conservative forces and example...
JEE main - Physics
Asked by arivaryakashyap | 23 Apr, 2024, 10:40: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by ratnadeep.dmr003 | 21 Apr, 2024, 11:06: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by ksahu8511 | 19 Apr, 2024, 11:55: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by mohammedimroz | 13 Apr, 2024, 09:48: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
ANSWERED BY EXPERT
