CBSE Class 10 - Areas of Similar Triangles Videos
Areas of similar triangles
This video explains the relation between the area of similar triangles and their corresponding sides and also solves problems related to them.
More videos from this chapter
View All-
find area

- The areas of two similar triangles are 49 cm2 and 64 cm2 respectively. The ratio of their corresponding sides is ____.
-
pl solve this sum
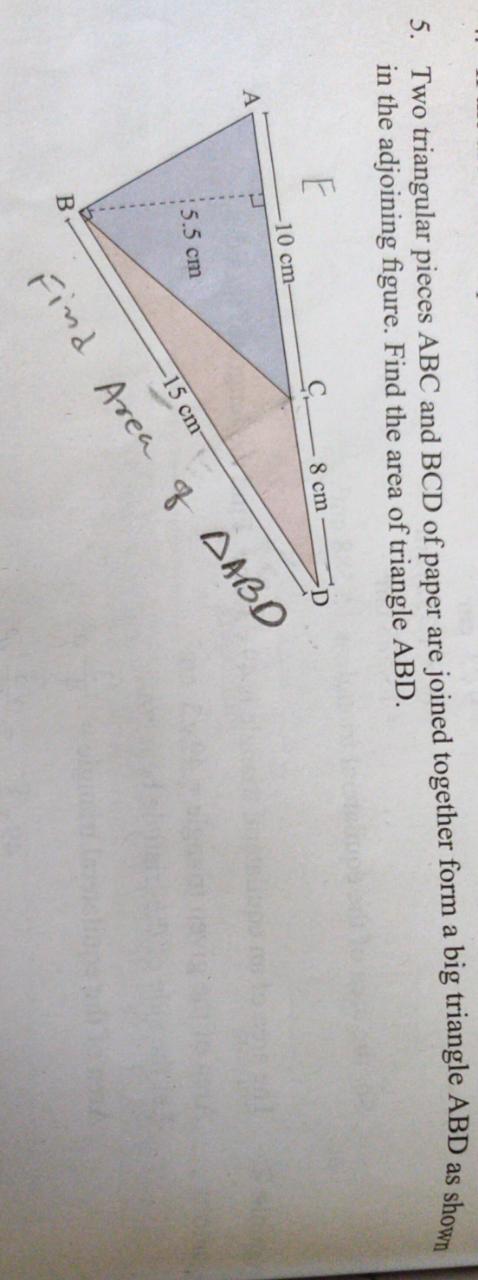
- Ij triangle ABC and BDE are equilateral triangles where D is the mid point of BC find the ratio of areas of triangle ABC BDE
-
Two chords AB and CD of a circle meet at E inside the circle as shown in the figure, such that
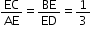 ,
, 
- Perimeters of two similar triangles ABC and DEF are in the ratio 3 : 4. Prove that the ratio of their areas is 9 : 16
- Perimeters of two similar triangles ABC and PQR are in the ratio 4 : 5. If the sum of their areas is 164 cm2, find the area of each triangle.
- The areas of two similar triangles ABC and PQR are in the ratio 4 : 9. If the sum of the perimeters is 30 m, find the perimeter of each triangle.
- A student needs 5 paper triangles for some craft work such that side of the second triangle are twice the sides of the first triangle, sides of the third triangle are twice the sides of the second triangle and so on.. Find the ratio of areas of the first and the fifth triangles.
- An equilateral triangle is based on the side of a square of area 64 sq. cm and another on the diagonal of the same square. Find the ratio of their areas.