CBSE Class 10 Answered
Perimeters of two similar triangles ABC and PQR are in the ratio 4 : 5. If the sum of their areas is 164 cm2, find the area of each triangle.
Asked by Topperlearning User | 03 Oct, 2017, 13:30: PM
Since triangles ABC and PQR are similar ,
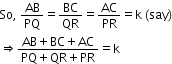
So according to question 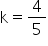 .
.
Let a side of triangle ABC be 4y and that of PQR is 5y.
We know that for two similar triangles the ratio of areas is equal to the ratio of squares of their corresponding sides.
Let the area of triangle ABC is S and that of triangle PQR is S’.
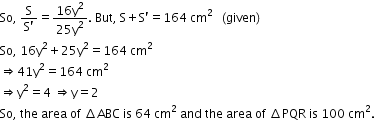
Answered by | 03 Oct, 2017, 15:30: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by priyanujt35 | 27 Jul, 2020, 09:13: AM
CBSE 10 - Maths
Asked by NSSORATHIYA sorathiya | 08 Mar, 2020, 10:16: AM
CBSE 10 - Maths
Asked by Sangsangapalian | 21 Sep, 2019, 09:34: AM
CBSE 10 - Maths
Asked by Topperlearning User | 05 Oct, 2017, 08:12: AM
CBSE 10 - Maths
Asked by Topperlearning User | 03 Oct, 2017, 13:29: PM
CBSE 10 - Maths
Asked by Topperlearning User | 03 Oct, 2017, 13:30: PM
CBSE 10 - Maths
Asked by Topperlearning User | 03 Oct, 2017, 13:32: PM
CBSE 10 - Maths
Asked by Topperlearning User | 03 Oct, 2017, 13:32: PM
CBSE 10 - Maths
Asked by Topperlearning User | 03 Oct, 2017, 13:36: PM











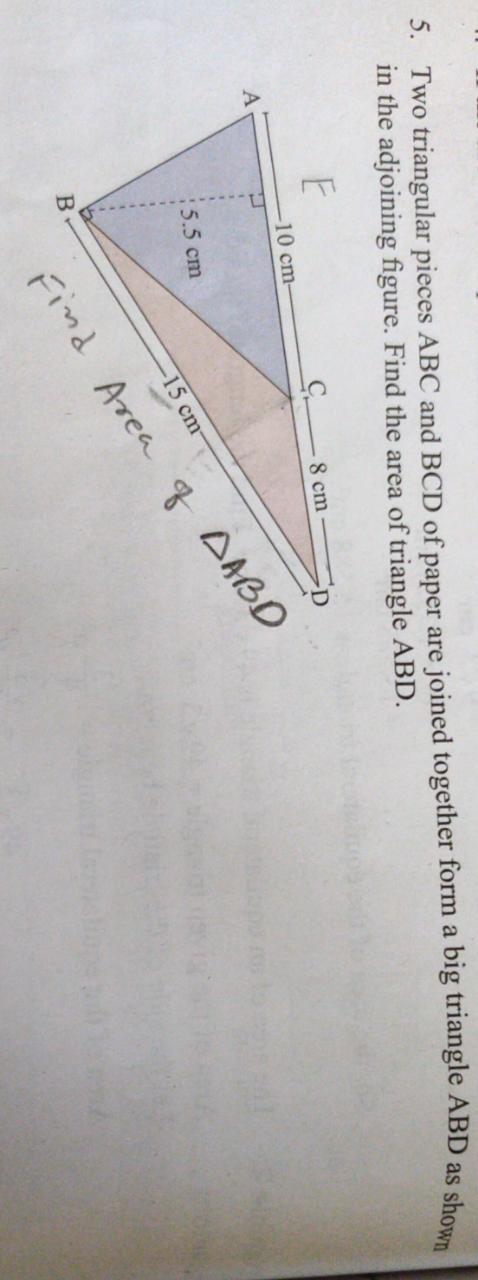
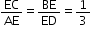 ,
, 
