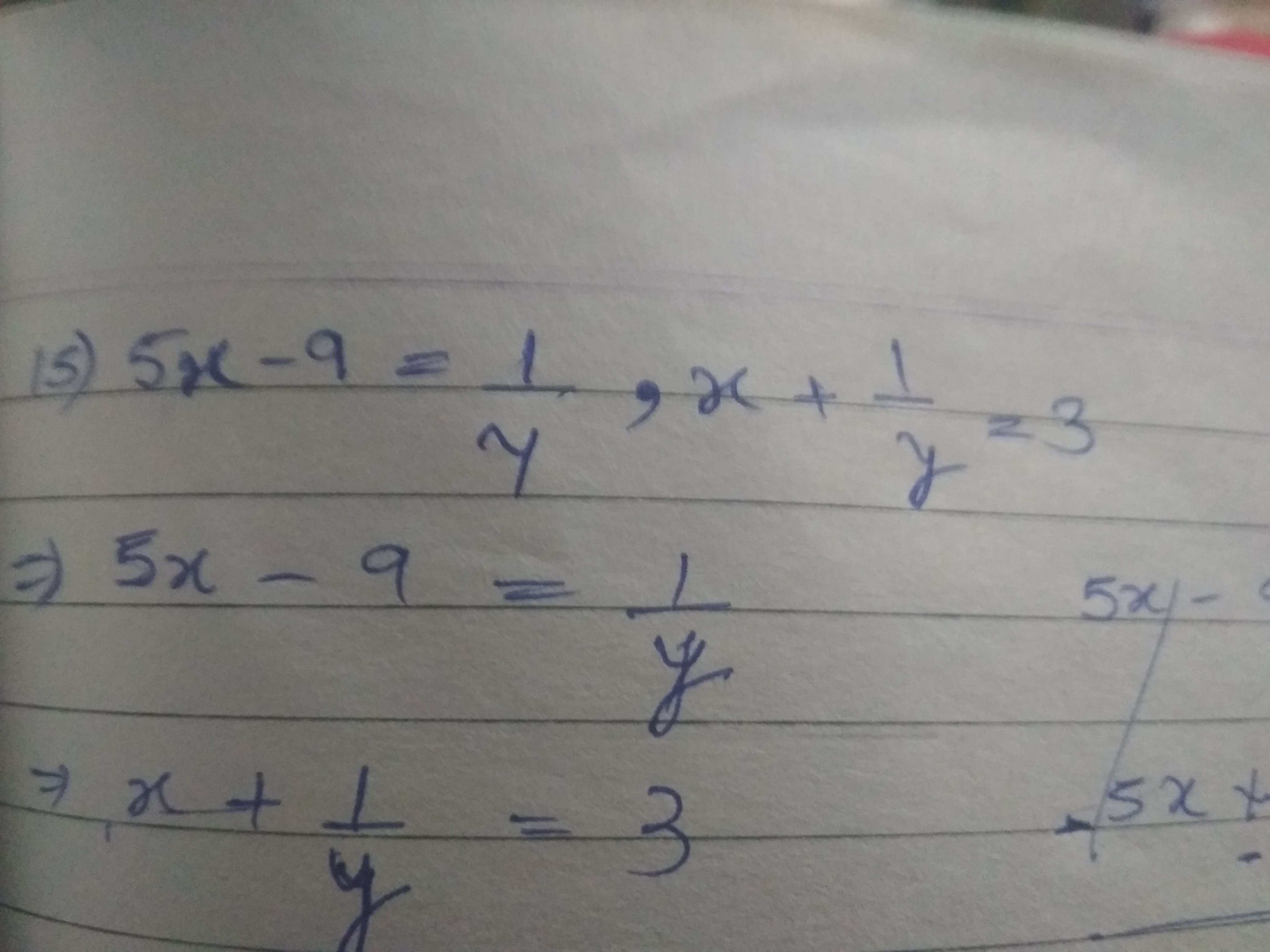Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

ICSE Class 9 Answered

When a two digit number is divided by the sum of its digits, the quotient is 7. If the ten's digit is diminished by twice the unit's digit, the remainder is zero. What is the number?
Asked by hemanginivyas92.9spicertl | 28 Jul, 2020, 17:14: PM
answered-by-expert Expert Answer
Let the ten's and unit's digits be respectively x and y
As per the question, we have
10x+y=7(x+y)
10x+y=7x+7y
3x-6y=0
x-2y=0 ... (i)
And, x-2y=0 ...(ii)
This gives us two same equations and so we can't find the unique values for x and y.
The question should be:
When a two digit number is divided by the sum of its digits, the quotient is 8. If the ten's digit is diminished by thrice the unit's digit, the remainder is zero. What is the number?
Solution:
Taking x and y as the the ten's and unit's digits respectively, we have
2x - 7y = 0 ...(i)
And, x - 3y = 1 ... (ii)
Solving (i) and (ii), we get
x = 7 and y = 2
Hence, the required number is 72.
Answered by Renu Varma | 29 Jul, 2020, 11:58: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
ICSE 9 - Maths
if 10y=7x-4 and 12x+18y=1; find the values of 4x+6y and 8y-x by elimnation by equating coefficient
Asked by kuardamanpreet934 | 26 Jun, 2024, 11:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
algebra question 15
question image
Asked by praveensaxena2009 | 28 May, 2022, 15:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
the some of the numerator and denominator of a fraction is 2 more than twice the numerator if the numerator and the denominator are reduced by 3 thay are in ratio 3:4 find the fraction
Asked by rrajsingh694 | 28 Jul, 2021, 13:56: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
2x-3Y-13=0;3X+5Y=16 stimulation method
Asked by kumarijanvi242004 | 28 Feb, 2021, 09:04: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
X+y=6 X-y=4 Find xy
Asked by Anandusree73 | 06 Jan, 2021, 16:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
1. 8x+5y=9   3x+2y=4    linear equation
Asked by kcbhuvan94 | 23 Sep, 2020, 15:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
3x + 4y =10 and 2x - 2y = 2
Asked by sannidhraj2004 | 16 Sep, 2020, 11:15: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
When a two digit number is divided by the sum of its digits, the quotient is 7. If the ten's digit is diminished by twice the unit's digit, the remainder is zero. What is the number?
Asked by hemanginivyas92.9spicertl | 28 Jul, 2020, 17:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
solve 4/X + 3/4=2 , 3/X - 2/4=5 by elimination method
Asked by deepvishal771 | 27 Jul, 2020, 11:26: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 9 - Maths
How to solve By elimination method table attributes columnalign left end attributes row cell 6 x plus 5 y equals 5 end cell row cell 2 x minus 27 equals 11 y end cell end table
Asked by eshaanbayale51.9spicertl | 02 Jun, 2020, 13:46: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt