CBSE Class 10 Answered

According to the division algorithm, if p(x) and g(x) are two polynomials with g(x) 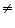 0, then we can find polynomials q(x) and r(x) such that
p(x) = g(x) x q(x) + r(x), where r(x) = 0 or degree of r(x) < degree of g(x).

(i)    Degree of quotient will be equal to degree of dividend when divisor is constant.
Let us consider the division of 18x² + 3x + 9  by 3.
Here, p(x) = 18x² + 3x + 9  and g(x) = 3
q(x) = 6x² + x + 3  and r(x) = 0
Here, degree of p(x) and q(x) is the same which is 2.


Checking:
p(x) = g(x) x q(x) + r(x)

 

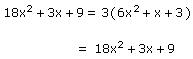
Thus, the division algorithm is satisfied.

(ii)    Let us consider the division of 2x⁴ + 2x by 2x³,
Here, p(x) = 2x⁴ + 2x and g(x) = 2x³
q(x) = x and r(x) = 2x
Clearly, the degree of q(x) and r(x) is the same which is 1.

Checking,
p(x) = g(x) x q(x) + r(x)
2x⁴ + 2x =  (2x³ ) x x  + 2x
2x⁴ + 2x = 2x⁴ + 2x
Thus, the division algorithm is satisfied.

(iii)    Degree of remainder will be 0 when remainder obtained on division is a constant.
Let us consider the division of 10x³ + 3 by 5x².
Here, p(x) = 10x³ + 3 and g(x) = 5x²
q(x) = 2x and r(x) = 3
Clearly, the degree of r(x) is 0.

Checking:
p(x) = g(x) x q(x) + r(x)
10x³ + 3 = (5x² ) x 2x  +  3
10x³ + 3 = 10x³ + 3
Thus, the division algorithm is satisfied.

Concept insight: In order to answer such type of questions, one should remember the division algorithm. Also, remember the condition on the remainder polynomial r(x). The polynomial r(x) is either 0 or its degree is strictly less than g(x). The answer may not be unique in all the cases because there can be multiple polynomials which satisfies  the given conditions.