Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

If two of the zeroes of the polynomial f(x)=x4-4x3-20x2+104x-105 are 3+√2 and 3-√2,then use the division algorithm to find the other zeroes of f(x).
Asked by saiprathumnan35 | 26 Jun, 2020, 07:17: PM
answered-by-expert Expert Answer
Given polynomial is f(x)=x4-4x3-20x2+104x-105
Two of its zeroes are 3+√2 and 3-√2
Therefore, [x - (3 + √2)] and [x - (3 - √2)] are the zeroes of f(x)
Therefore, [x - (3 + √2)][x - (3 - √2)] = [x-3-√2][x-3+√2] = x2 - 6x + 9 - 2 = x2 - 6x + 7  divides the polynomial f(x)
Using long division to divide f(x) by (x2 - 6x + 7), we get the quotient as x2 + 2x - 15
 
 
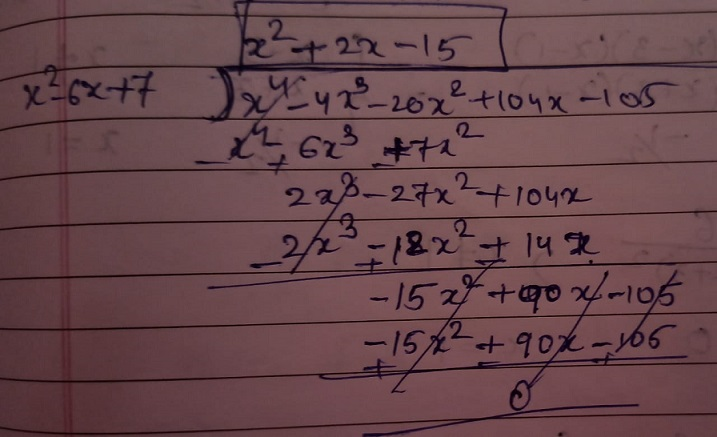
The other factor of f(x) is x2 + 2x - 15
x2 + 2x - 15 = x2 + 5x - 3x - 15 = x(x+5) - 3(x+5) = (x+5)(x-3)
Hence, the other two zeroes are -5 and 3.
Answered by Renu Varma | 29 Jun, 2020, 11:21: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test Subjective Questions Webinar Subjective Questions Pre Board Assessment
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
What should be added to the polynomial x^3 - 2x^2 -3x -4 so, that it is completely divisible by x^2 - x
Asked by mv716304 | 01 Apr, 2022, 05:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
x^2+2√2x-6
Asked by mahekk101 | 14 Sep, 2021, 08:24: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if the two zeros of quadratic polynomial 7x²-15x-k are reciprocals of each other the value of k?
question image
Asked by bhavikabhatia1125 | 03 Aug, 2021, 10:29: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If the polynomial 2x⁴ + x³ - 3x² +18x + 24 is divided by another polynomial x² + 3x - m and  the remainder comes out to be 4x + n. Find the value of m and n respectively.
Asked by Aasthaachd | 08 Jun, 2021, 01:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Divide x^4 -5x+6 by x^2 -2
Asked by rk4353620 | 05 Jun, 2021, 01:52: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Find whether 3x+2 is a factor of 3x^4+ 5x^3+ 13x-x^2 + 10
Asked by diyayadav1441 | 27 Jul, 2020, 03:59: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
If two of the zeroes of the polynomial f(x)=x4-4x3-20x2+104x-105 are 3+√2 and 3-√2,then use the division algorithm to find the other zeroes of f(x).
Asked by saiprathumnan35 | 26 Jun, 2020, 07:17: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
2x⁴+x³-14x²-15x-8 divide by x²+3x+2
Asked by Gurnoorsingh0852 | 03 Jun, 2020, 03:54: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Using division algorithm find the quotient and remainder of the following: I) x³-6x²+11x-6 by x²+x+1
Asked by renuneeraj2005 | 02 Jun, 2020, 11:00: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if m and n are divided by 4 then 2 and 3 are respectively the remainders find the remainder when m square + n square is divided by 4
question image
Asked by dash.ak35 | 08 Apr, 2020, 01:19: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt

Be a Top Scorer in the Exam with Test Series and Test Generator!

Enrol Now
×