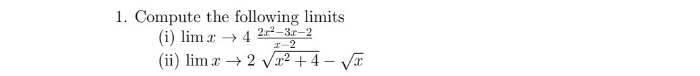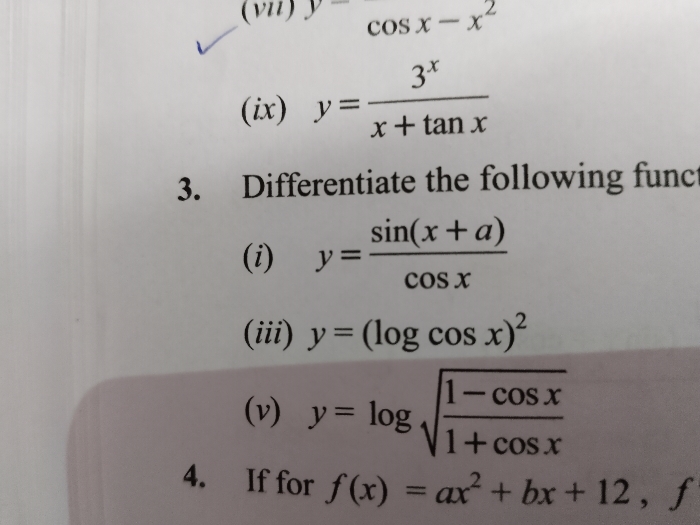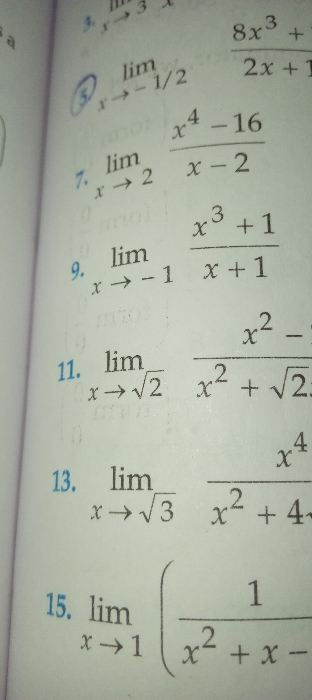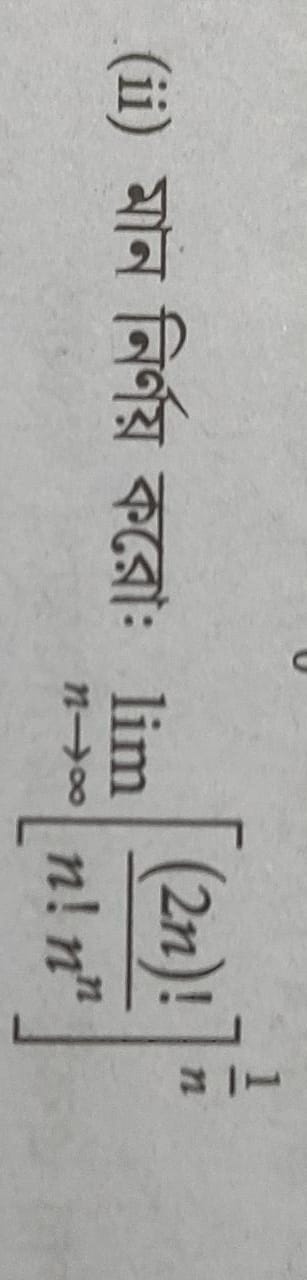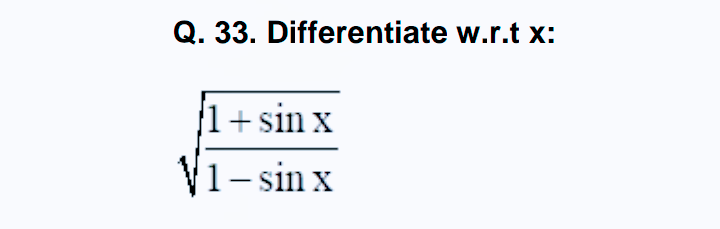CBSE Class 11-science Answered
What are L'HOPITAL'S RULES ?
EXPLAIN AND STATE WITH EXAMPLES.
Asked by advait2163 | 23 May, 2011, 09:18: PM
Expert Answer
In calculus, l'Hôpital's rule pronounced [lopi?tal] (also called Bernoulli's rule) uses derivatives to help evaluate limits involving indeterminate forms. Application (or repeated application) of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit.
In its simplest form, l'Hôpital's rule states that for functions f and g:
If 
or 
and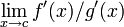 
exists,
then 
The differentiation of the numerator and denominator often simplifies the quotient and/or converts it to a determinate form, allowing the limit to be evaluated more easily.
For more Information try the following link:
en.wikipedia.org/wiki/L'Hôpital's_rule
Answered by | 24 May, 2011, 08:36: AM
Concept Videos
-
...
This video explains the intuitive idea of limit of a function, rules of alg... -
Limit of rational functions
This video covers examples related to finding the limit of rational functio... -
Limits of Trigonometric Functions
This video explains the use of sandwich/Squeeze Theorem to find the limit a... -
Meaning of Derivatives
This video explains derivatives as rate of change of distance function and ... -
Derivative of linear combination of functions using con ...
Derivative of linear combination of functions using constant multiple, sum ...
CBSE 11-science - Maths
Asked by kanishkatutejasirsa | 09 Mar, 2024, 11:08: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by ns091764623 | 03 Mar, 2024, 08:33: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by pndash1974 | 08 Nov, 2023, 08:40: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by amisharanjan14 | 30 Sep, 2023, 07:28: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by sdmbotch1123 | 18 Jan, 2023, 11:02: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by kushik.jnp2025 | 15 Jan, 2023, 12:00: AM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by ankitkanjilal409 | 30 Dec, 2022, 08:25: PM
ANSWERED BY EXPERTCBSE 11-science - Maths
Asked by huzaifashangroo | 28 Dec, 2022, 06:57: PM
ANSWERED BY EXPERT
