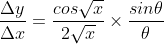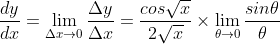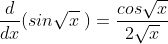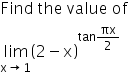CBSE Class 11-science Answered

Qn. # (26)

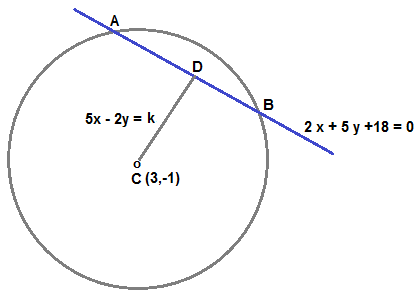
Let C(3,-1) be centre of circle . AB is chord of length 6 cm and its equation is  2 x+ 5y +18 = 0

Let CD be perpendicular to AB ,

Since CD is perpendicular to AB , equation of CD is  5x -2y = k , where k is constant to be determined.

Line CD is passing through C (3, -1) . Hence we get equation of line as

5(3) - 2 (-1) = k  or  k = 17

Point of intersection is determined by solving the line equations as given below

2 x + 5 y = -18

5x - 2y = 17

By solving above equations , we get

x = 49/29  ;  y = -124/29  ;

Point of intersection is  D ( 49/29 , -124/29 )

Length of CD is

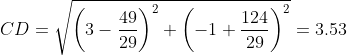
Radius R is calculated as

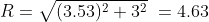cm

If (h, k ) is centre of circle and R is radius of circle , then equation of circle is

(x-h)² + ( y-k)² = R²

Hence equaion of circle with centre ( 3, -1) and radius 4.63 cm is

(x-3)² + (y+1)² = (4.63)² = 21.4

-----------------------------------------------------------

Qn. # 28

y = √x

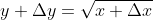
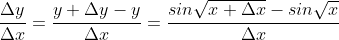  .........................(1)

If Δx → 0 , then

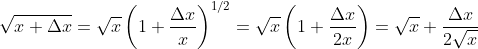......................(2)

In above approximation, higher powers of Δx are neglected in the series expansion

  ..................(3)

Using eqn.(3) , we rewrite eqn.(2) as

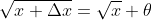
Hence we rewrite eqn.(1) as

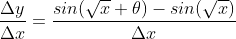
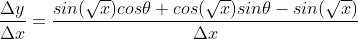...............................(4)

if Δx → 0 , then we get from eqn.(3) ,  θ → 0  and cosθ → 1

From eqn.(3) , we can write Δx = 2 √x θ

Hence eqn.(4) becomes