Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

two springs are connected end to end,same load is used.you need to relate spring constant of one spring with other.what is the effective spring constants in terms of k1 and k2.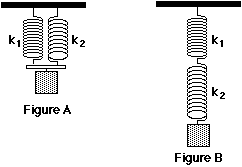
Asked by archana | 18 Sep, 2015, 08:18: AM
answered-by-expert Expert Answer
Springs connected in series (Figure B):
Two strings having individual spring stiffness of k1 and k2 units connected in series as shown in the figure.
Since each spring supports the load W, the total deflection of the spring will be the sum of the deflections of the individual springs. 
Deflection of first spring, y1=W/k1 and that of the second spring, y2=W/k2.
As the deflection of the spring with constant k is given by, y=y1+y2.
Therefore, W/k=W/k1+W/k2 or 1/k=1/k1+1/k2 or effective of the spring, k=k1k2/(k1+k2).
 
Springs connected in parallel (Figure A):
Two strings having individual spring stiffness k1 and k2 are connected in parallel.
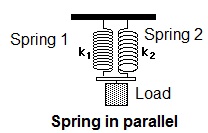
Since the load is shared by the two springs jointly the sum of the loads W1 and W2 taken by individual springs must be equal to the axial load W applied on the composite spring.
Thus the same deflection 'y' of the two springs the load taken by the individual springs will be: 
Load taken by first spring, W1=k1y, and the load taken by the second spring, W2=k2y.
With k as the stiffness of the spring the load taken by the spring is W=ky.
W=W1+W2, we get, ky=k1y+k2y
The effective of the springs connected in parallel is given by, k=k1+k2.
Answered by Faiza Lambe | 18 Sep, 2015, 11:25: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Physics
why is force attractive when the separation between body and force increases and potential increases and vice versa? why is force repulsive when separation between body and force increases and potential decreases? if PE/force is negative why attraction and if PE/force is positive why there is repulsion? pls explain and prove the above points with suitable examples.
Asked by kaziryan.05 | 22 May, 2021, 11:38: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
State the law of conservation of energy.
Asked by Topperlearning User | 09 Jul, 2014, 10:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
An airplane with a mass of 2000 kg sinks 1000 metres moving forward a horizontal distance of 10,000 metres. What will be its new potential energy? (Take g = 10 m/s2)
Asked by Topperlearning User | 08 Jul, 2014, 10:19: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
What is the source of the kinetic energy of the falling rain drop?
Asked by Topperlearning User | 08 Jul, 2014, 10:32: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Explain why the water at the foot of the waterfall is at different temperature from that at the top?
Asked by Topperlearning User | 08 Jul, 2014, 10:34: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A body is moving with the speed of 30 m/s. How high can it be lifted to gain an amount of potential energy equal to its kinetic energy. (Take g = 10 m/s2)
Asked by Topperlearning User | 08 Jul, 2014, 10:36: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
A body falling from the height of 10 m rebounds from the hard surface. It loses 20% of its energy in impact. What is the height to which it would raise after the impact and where this energy goes after hitting the surface?
Asked by Topperlearning User | 08 Jul, 2014, 10:45: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Two springs have force constants k1 and k2 where k1 > k2. On which spring, more work is done if they are stretched by the same magnitude of force. 
Asked by Topperlearning User | 08 Jul, 2014, 10:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
If a block attached to a spring (whose one end is fixed) is pulled up to a distance xo and released, the amplitude of its motion cannot exceed Syntax error from line 1 column 49 to line 1 column 73. Unexpected '<mstyle '. why?
Asked by Topperlearning User | 08 Jul, 2014, 10:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Physics
Draw a plot of spring force versus displacement x. Hence find an expression for the P.E of an elastic spring.
Asked by Topperlearning User | 08 Jul, 2014, 11:08: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×