CBSE Class 10 Answered
To find the area of a quadrilateral we divide it into two triangles and then find the area of each triangle with the help of the triangle formula and add them. But I have noticed a pattern in them. For ex:
Find the area of the quadrilateral formed by joining the points - A(-4,-2), B(-3,-5), C(3,-2), D(2,3).
In questions like this, we get the area correctly only if we add the areas of traingles ABC and ACD. We don't get the correct answer if we add them in a different manner, say triangle ABC and ADC etc. We can even check this on the above question. We get the answer only if add the triangles ABC and ACD and not in some other way. Is there a reason for this? If yes, please explain.
Asked by Sthitaprajna Mishra | 17 Mar, 2015, 12:27: PM
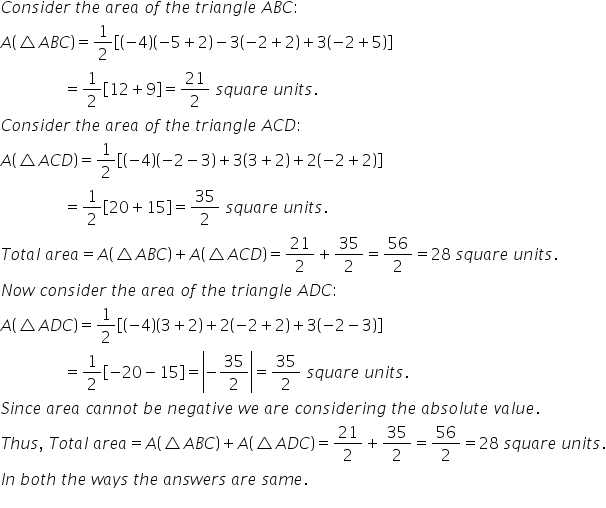
Answered by Vimala Ramamurthy | 18 Mar, 2015, 10:23: AM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by kadaramyadav | 02 Nov, 2023, 11:02: PM
CBSE 10 - Maths
Asked by priyankakiran2017 | 25 May, 2022, 06:59: AM
CBSE 10 - Maths
Asked by priyankakiran2017 | 25 May, 2022, 06:58: AM
CBSE 10 - Maths
Asked by jaiharekrushna75 | 11 Sep, 2020, 11:56: AM
CBSE 10 - Maths
Asked by dvijaybs45 | 07 Sep, 2020, 08:57: PM
CBSE 10 - Maths
Asked by nijurajeev7276 | 08 Jan, 2020, 09:52: AM
CBSE 10 - Maths
Asked by priyalpathak06 | 05 May, 2019, 11:55: PM