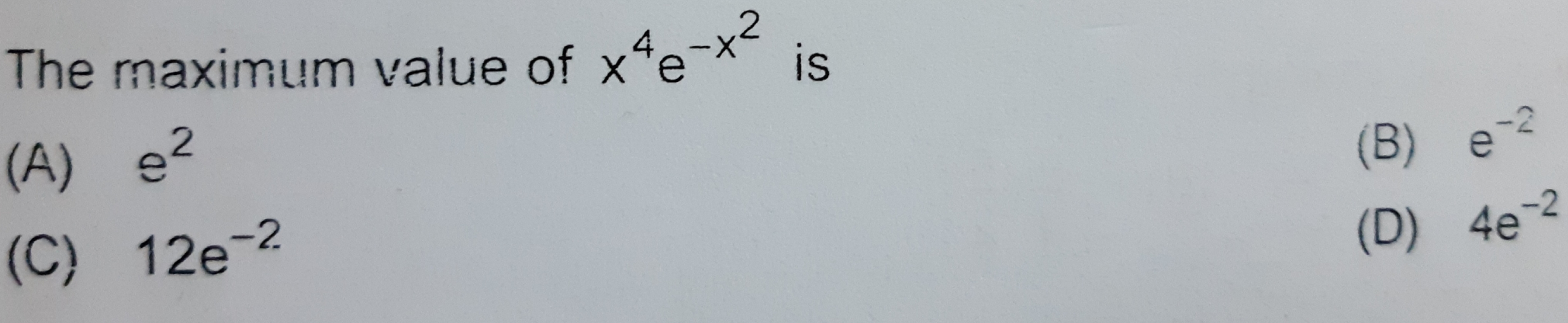CBSE Class 12-science Answered
The maximum and the minimum values, if any of the following functions
f (x) = |x + 3| for all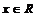 
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
Expert Answer
We have
f (x) = |x + 3| for all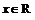 
Now, |x + 3|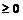 
for all
for all 
for all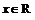 So, the minimum value of f (x) is 0, which it attains at x = — 3
Clearly, f (x) = |x + 3 | does not have the maximum value
Answered by | 04 Jun, 2014, 15:23: PM
Concept Videos
-
Maxima and Minima by first derivative test
This video explains how to solve algebraic and trigonometric problems of Ma... -
Algebraic and trigonometric problems of maxima and mini ...
Understand and solve algebraic and trigonometric problems of maxima and min... -
Maxima and Minima using first derivative test ...
This video covers examples and concepts related to algebraic and trigonomet...
CBSE 12-science - Maths
Asked by shubh31122006 | 23 Dec, 2023, 14:27: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by lailavafra08 | 26 Oct, 2023, 19:24: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by dineshchem108 | 09 Oct, 2019, 19:04: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by haroonrashidgkp | 08 Sep, 2018, 16:14: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
The maximum and the minimum values, if any of the following functions
f (x) = –| x – 1 | + 5 for all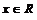 
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
ANSWERED BY EXPERTCBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
ANSWERED BY EXPERT
