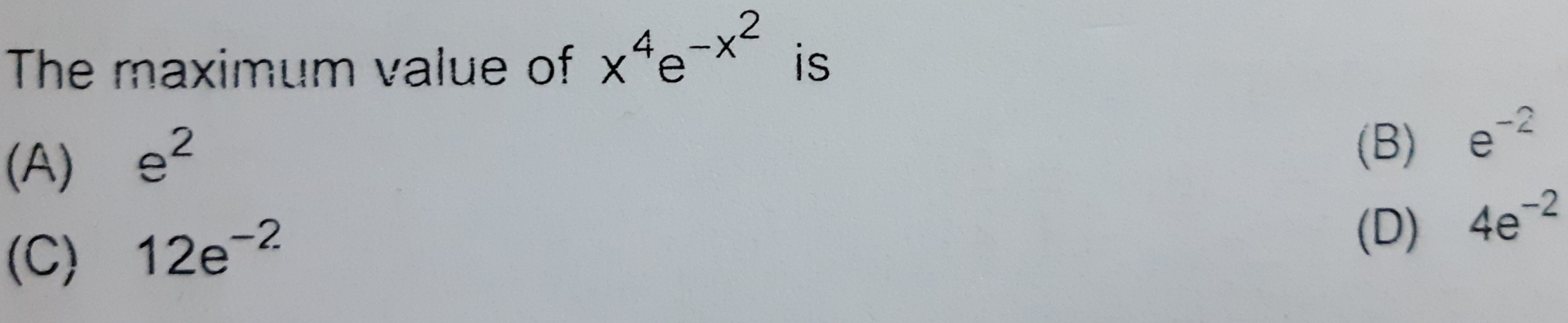CBSE Class 12-science Answered
An inverted cone has a depth of 40 cm and a base radius of 5cm. Water is poured into it at a rate of 1.5 cubic centimetres /minute . find the rate at which the level of water in cone is rising when the depth is 4cm.
explain in great detail
Asked by haroonrashidgkp | 08 Sep, 2018, 16:14: PM
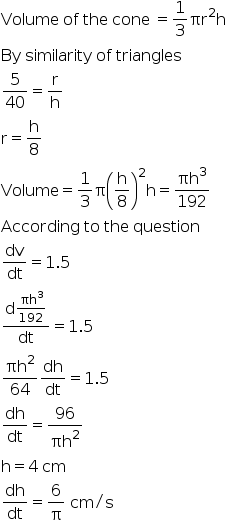
Answered by Sneha shidid | 09 Sep, 2018, 18:22: PM
Concept Videos
CBSE 12-science - Maths
Asked by shubh31122006 | 23 Dec, 2023, 14:27: PM
CBSE 12-science - Maths
Asked by lailavafra08 | 26 Oct, 2023, 19:24: PM
CBSE 12-science - Maths
Asked by dineshchem108 | 09 Oct, 2019, 19:04: PM
CBSE 12-science - Maths
Asked by haroonrashidgkp | 08 Sep, 2018, 16:14: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
The maximum and the minimum values, if any of the following functions
f (x) = –| x – 1 | + 5 for all 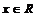
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 13:23: PM