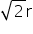CBSE Class 12-science Answered
Suppose a company manufactures x units.
And the cost of manufacturing these x units comes out to be a cost function given as c(x)=2x3 -60x2 +1500. Definitely the company would like to minimise its cost to attain maximum profit. So here we would like to know how many units should be manufactured to get minimum cost,
Asked by Topperlearning User | 19 Aug, 2014, 08:45: AM
We will find out that using our second derivative test.
For that we need to differentiate this function
We get 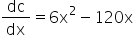
Taking 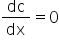 to find extreme points
to find extreme points
6x(x - 20)=0
Since x≠0 because x=0 means no production so we take x=20.
Now, to check whether this will maximise or minimise cost. We need to find the second derivative, which is 
This second derivative at x=20 is
12 x 20 – 120 = 240 – 120 = 120
which is positive.
This indicates that x=20 is a point of local minima.
Hence, we can say cost is minimum when 20 units of items are produced.
Answered by | 19 Aug, 2014, 10:45: AM
Concept Videos
CBSE 12-science - Maths
Asked by srisrinivasa.mcrl | 04 Feb, 2024, 10:39: AM
CBSE 12-science - Maths
Asked by Ronitupadhyay13 | 20 Dec, 2019, 00:28: AM
CBSE 12-science - Maths
Asked by tv2000in | 28 May, 2019, 00:02: AM
CBSE 12-science - Maths
Asked by Kchawla94 | 02 Apr, 2019, 18:45: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 21 Aug, 2014, 13:22: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:25: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 21 Aug, 2014, 12:21: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 08:45: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:38: AM




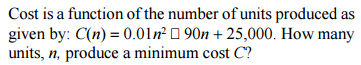

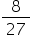 of the volume of the sphere.
of the volume of the sphere.