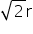CBSE Class 12-science Answered
Suppose a certain sheet of metal is given and we need to make a right circular cylinder tin out of it such that it contains maximum quantity of oil. Here we assume no metal is wasted.
Asked by Topperlearning User | 19 Aug, 2014, 09:12: AM

Answered by | 19 Aug, 2014, 11:12: AM
Concept Videos
CBSE 12-science - Maths
Asked by srisrinivasa.mcrl | 04 Feb, 2024, 10:39: AM
CBSE 12-science - Maths
Asked by Ronitupadhyay13 | 20 Dec, 2019, 00:28: AM
CBSE 12-science - Maths
Asked by tv2000in | 28 May, 2019, 00:02: AM
CBSE 12-science - Maths
Asked by Kchawla94 | 02 Apr, 2019, 18:45: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 21 Aug, 2014, 13:22: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:25: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 21 Aug, 2014, 12:21: PM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 08:45: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:12: AM
CBSE 12-science - Maths
Asked by Topperlearning User | 19 Aug, 2014, 09:38: AM





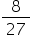 of the volume of the sphere.
of the volume of the sphere.