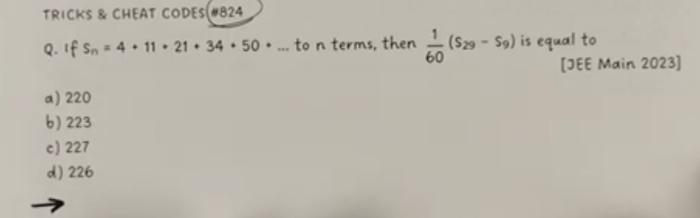JEE Class main Answered
solution
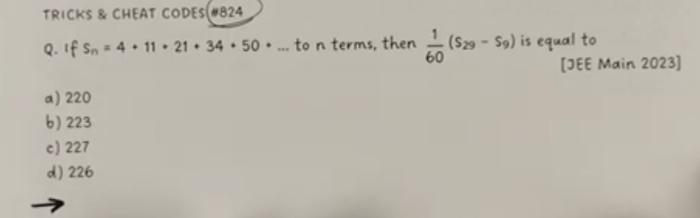
Asked by 20sanjaykoley20 | 19 Dec, 2023, 00:57: AM

Each term in above sum is written as
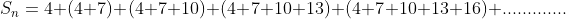
Each term is arithmetic progression ( 4+7+10+........... ) . Number of terms in arithmetic progression (A.P.)equals term number .
For example first term of given sum has only one term of A.P. , second term of given sum fas two terms of A.P etc..
Given sum is written as
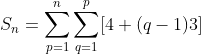
inner sum is written as

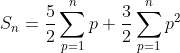
Hence in above sum , first term is sum of natural numbers and second term is sum of squares
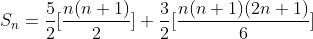
Above expression is simplified as
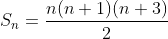
Hence we get , S29 = (1/2) ( 29 × 30 × 32) and S9 = (1/2) ( 9 × 10 × 12)
S29 - S9 = 60 × [ 232 - 9 ]
(1/60) [ S29 - S9 ] = 223
Answered by Thiyagarajan K | 19 Dec, 2023, 11:53: AM
JEE main - Maths
Asked by vishalsarap0022 | 19 May, 2024, 10:30: AM
JEE main - Maths
Asked by obravickykumar50 | 07 May, 2024, 09:27: AM
JEE main - Maths
Asked by vishwajeetsinghrajput2018 | 17 Mar, 2024, 00:27: AM
JEE main - Maths
Asked by sabeenashaik575 | 09 Jan, 2024, 09:53: AM
JEE main - Maths
Asked by kunmunkumar08032008 | 08 Oct, 2023, 13:15: PM
JEE main - Maths
Asked by nitinsolanki14102001 | 16 Sep, 2023, 15:01: PM
JEE main - Maths
Asked by joanmaria916 | 08 Jul, 2023, 16:37: PM
JEE main - Maths
Asked by vishnuramrs07 | 30 May, 2023, 21:05: PM