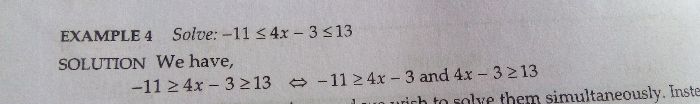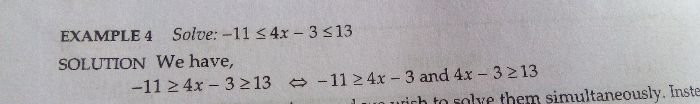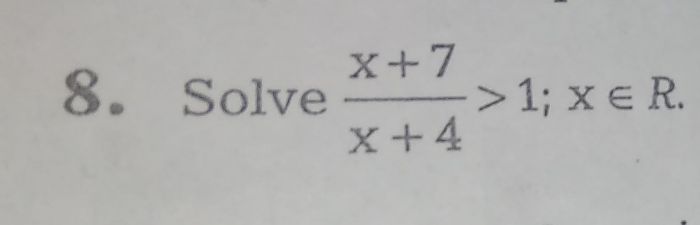Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

sir this is quadratic equation problem
Asked by Aravindh Nandha Raj s | 27 May, 2013, 06:04: PM
answered-by-expert Expert Answer
Let f(x) = (x-a)(x-c)+2(x-b)(x-d)
f(a) = 2(a-b)(a-d) > 0
f(b) = (b-a)(b-c) < 0
f(c) = 2(c-b)(c-d) < 0
f(d) = (d-a)(d-c) > 0

In going from a to b, f(x) goes from being greater than zero to being less than zero. Because f(x) is continuous, there is some a < x < b, such that f(x) = 0.
Similarly, there is some c < x < d, such that f(x) = 0. 

That is, there is one real root between a and b and another real root between c and d. Because f(x) is a polynomial of degree two, there are a total of two roots and they will be distinct
Answered by | 28 May, 2013, 02:37: AM

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
The length of a rectangle is 5 more than the 2 times of its breadth. If the perimeter of the rectangle is at least 640 cm. Find the minimum value of its breadth.  
Asked by manthanpal3 | 28 Jun, 2023, 12:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
In connection with my previous doubt. Sir/Ma'am, but why are the signs of the inequalities reversed in the 2 inequations in the RD solution?
question image
Asked by youdhustu | 25 Jun, 2022, 01:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
How to split this double inequality into 2 inequations and get the solution set of the system of inequations by intersection method? I didn't understand how to split it into 2 inequations.
question image
Asked by youdhustu | 25 Jun, 2022, 12:10: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
A= {(x, y): x, y∈ I, X≥0, y≥0 and 5x + 6y ≤40} B= {(x, y): x, y∈ l, x≥0, y≥0 and 6x + 5y ≤ 40} Where I denotes set of integers, then n(A∩B) is
Asked by mohvijayjain12 | 22 Jun, 2022, 11:07: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
solve
question image
Asked by akshaybhai120 | 27 May, 2022, 06:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find values of x for:- ||x-1|-2|=|x-3|
question image
Asked by 9377777388ts | 09 Aug, 2020, 05:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
3x+2y>5,y>2
Asked by swajaydixit04 | 19 Jun, 2020, 10:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find x .
question image
Asked by anshr8260 | 24 May, 2020, 07:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If we know two inequalities for a number k, how should we combine them? Like ( k is greater than 2) and ( {k+6}{k-4} is greater than 0). What will be k ultimately?
Asked by drhimasingh | 23 Apr, 2020, 11:34: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Solve (x+7/x+4)>1;x belongs to R
question image
Asked by sankarprasadroy1187 | 11 Feb, 2020, 07:03: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×