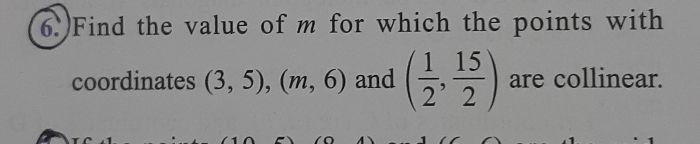Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

Show that the points A (a, b+c), B (b, c + a) and C (c, a + b) are collinear.
Asked by Topperlearning User | 24 Nov, 2013, 05:23: AM
answered-by-expert Expert Answer
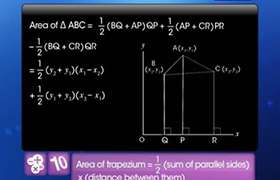
If the given points are collinear then the area of the triangle formed by joining these points is zero.
Here, x1 = a, y1 = b + c; x2 = b, y2 = c + a; x3 = c, y3 = a + b.
Substituting the values in the formula for area of a triangle, you get
ac - ab + ab - bc + bc - ac = 0
Hence the given points are collinear.
Answered by | 24 Nov, 2013, 07:23: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
find the centroid of the triangles with vertices: (-1,3),(6,-3) and (-3,6)
Asked by kadaramyadav | 02 Nov, 2023, 11:02: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
draw the graph of the equations y=x and x=1. Hence , find the area of the triangle formed by these two lines and the x-axis
Asked by priyankakiran2017 | 25 May, 2022, 06:59: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
name the special quadrilateral formed by the lines x=2,x=-2 ,y=3 and y=-2and hence find its area
Asked by priyankakiran2017 | 25 May, 2022, 06:58: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
solve
question image
Asked by Trisha Gupta | 03 Nov, 2021, 12:45: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
question
question image
Asked by arindeep.singh | 17 Sep, 2020, 11:19: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
in each of the following find the value of k for which the points are collinear . 1) (7,-2), (5,1) ,(3,k)
Asked by jaiharekrushna75 | 11 Sep, 2020, 11:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
In each of the following, find the value of a for which the given points are collinear.  (ii) (a-3-2a), (-a+1,2a) and (-4-a,6-2a)
Asked by dvijaybs45 | 07 Sep, 2020, 08:57: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The 27th question...
question image
Asked by subbukum | 13 Feb, 2020, 12:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Find the area of the Triangle ABC, with vertex A(1,-4) and midpoint of AB and AC as X(2,-1) and Y(0,-4) respectively.  
Asked by nijurajeev7276 | 08 Jan, 2020, 09:52: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
in RD Sharma's solution , ex.6.5 , Q.24, why we have taken the value 1/2 with both positive and negative sign. What is the reason for doing this?????
Asked by priyalpathak06 | 05 May, 2019, 11:55: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×